Variational Bridge Constructs for Grey Box Modelling with Gaussian Processes

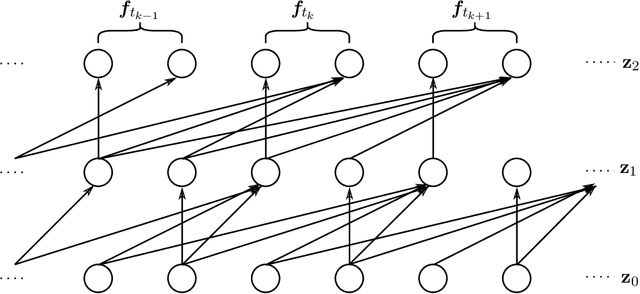
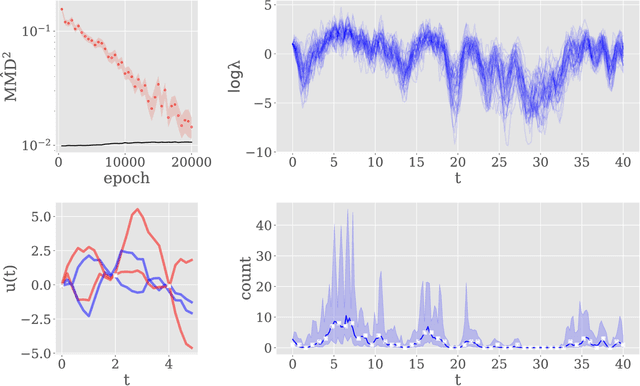
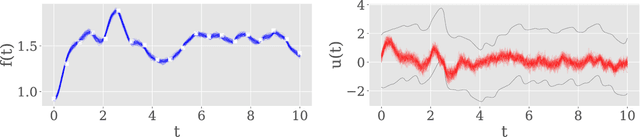
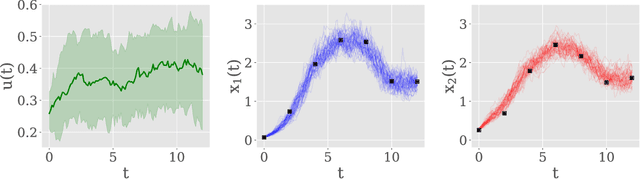
This paper introduces a method for inference of heterogeneous dynamical systems where part of the dynamics are known, in the form of an ordinary differential equation (ODEs), with some functional input that is unknown. Inference of such systems can be difficult, particularly when the dynamics are non-linear and the input is unknown. In this work, we place a Gaussian process (GP) prior over the input function which results in a stochastic It\^o process. Using an autoregressive variational approach, we simulate samples from the resulting process and conform them to the dynamics of the system, conditioned on some observation model. We apply the approach to non-linear ODEs to evaluate the method. As a simulation-based inference method, we also show how it can be extended to models with non-Gaussian likelihoods, such as count data.

Non-linear process convolutions for multi-output Gaussian processes

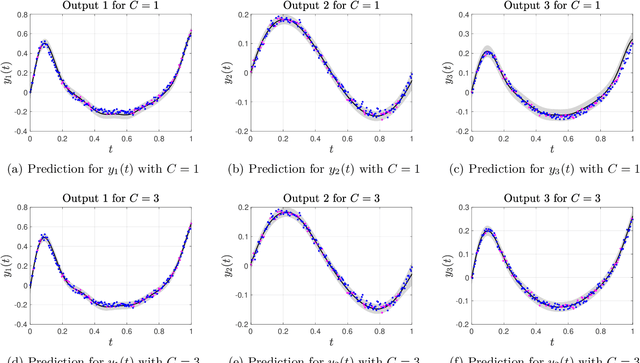
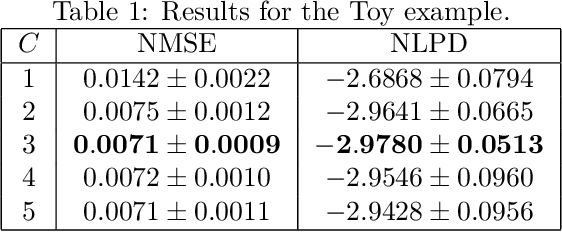
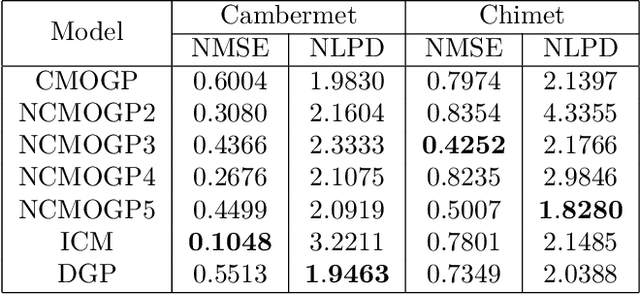
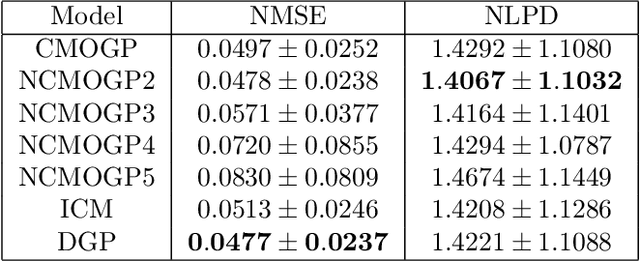
The paper introduces a non-linear version of the process convolution formalism for building covariance functions for multi-output Gaussian processes. The non-linearity is introduced via Volterra series, one series per each output. We provide closed-form expressions for the mean function and the covariance function of the approximated Gaussian process at the output of the Volterra series. The mean function and covariance function for the joint Gaussian process are derived using formulae for the product moments of Gaussian variables. We compare the performance of the non-linear model against the classical process convolution approach in one synthetic dataset and two real datasets.