Non-linear process convolutions for multi-output Gaussian processes

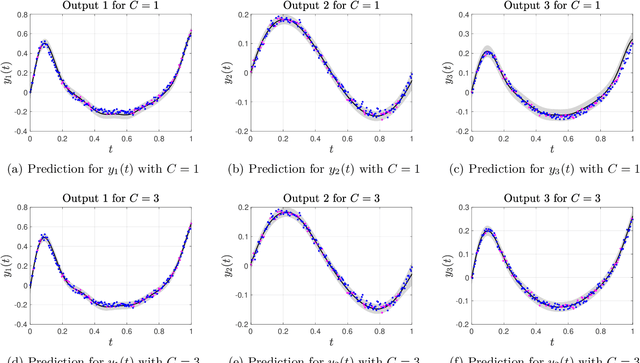
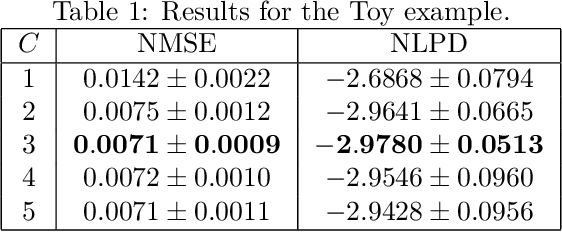
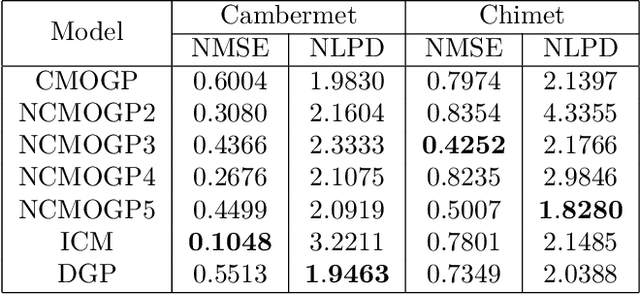
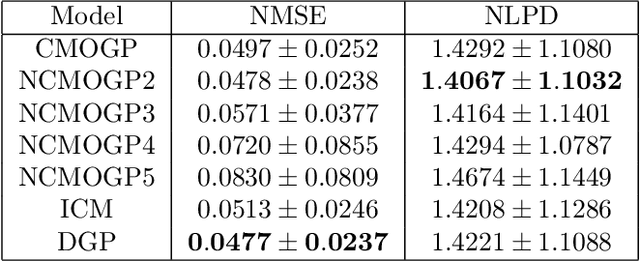
The paper introduces a non-linear version of the process convolution formalism for building covariance functions for multi-output Gaussian processes. The non-linearity is introduced via Volterra series, one series per each output. We provide closed-form expressions for the mean function and the covariance function of the approximated Gaussian process at the output of the Volterra series. The mean function and covariance function for the joint Gaussian process are derived using formulae for the product moments of Gaussian variables. We compare the performance of the non-linear model against the classical process convolution approach in one synthetic dataset and two real datasets.

Fast Kernel Approximations for Latent Force Models and Convolved Multiple-Output Gaussian processes

A latent force model is a Gaussian process with a covariance function inspired by a differential operator. Such covariance function is obtained by performing convolution integrals between Green's functions associated to the differential operators, and covariance functions associated to latent functions. In the classical formulation of latent force models, the covariance functions are obtained analytically by solving a double integral, leading to expressions that involve numerical solutions of different types of error functions. In consequence, the covariance matrix calculation is considerably expensive, because it requires the evaluation of one or more of these error functions. In this paper, we use random Fourier features to approximate the solution of these double integrals obtaining simpler analytical expressions for such covariance functions. We show experimental results using ordinary differential operators and provide an extension to build general kernel functions for convolved multiple output Gaussian processes.

Indian Buffet process for model selection in convolved multiple-output Gaussian processes

Multi-output Gaussian processes have received increasing attention during the last few years as a natural mechanism to extend the powerful flexibility of Gaussian processes to the setup of multiple output variables. The key point here is the ability to design kernel functions that allow exploiting the correlations between the outputs while fulfilling the positive definiteness requisite for the covariance function. Alternatives to construct these covariance functions are the linear model of coregionalization and process convolutions. Each of these methods demand the specification of the number of latent Gaussian process used to build the covariance function for the outputs. We propose in this paper, the use of an Indian Buffet process as a way to perform model selection over the number of latent Gaussian processes. This type of model is particularly important in the context of latent force models, where the latent forces are associated to physical quantities like protein profiles or latent forces in mechanical systems. We use variational inference to estimate posterior distributions over the variables involved, and show examples of the model performance over artificial data, a motion capture dataset, and a gene expression dataset.