Trajectory Tracking for UAVs: An Interpolating Control Approach

Building on our previous work, this paper investigates the effectiveness of interpolating control (IC) for real-time trajectory tracking. Unlike prior studies that focused on trajectory tracking itself or UAV stabilization control in simulation, we evaluate the performance of a modified extended IC (eIC) controller compared to Model Predictive Control (MPC) through both simulated and laboratory experiments with a remotely controlled UAV. The evaluation focuses on the computational efficiency and control quality of real-time UAV trajectory tracking compared to previous IC applications. The results demonstrate that the eIC controller achieves competitive performance compared to MPC while significantly reducing computational complexity, making it a promising alternative for resource-constrained platforms.

UAV Trajectory Planning with Path Processing

This paper examines the influence of initial guesses on trajectory planning for Unmanned Aerial Vehicles (UAVs) formulated in terms of Optimal Control Problem (OCP). The OCP is solved numerically using the Pseudospectral collocation method. Our approach leverages a path identified through Lazy Theta* and incorporates known constraints and a model of the UAV's behavior for the initial guess. Our findings indicate that a suitable initial guess has a beneficial influence on the planned trajectory. They also suggest promising directions for future research.

Mission Planner for UAV Battery Replacement

The paper presents a mission planner for an autonomous unmanned aerial vehicle (UAV) battery management system. The objective of the system is to plan replacements of the UAV's battery on the static battery management stations. The plan ensures that UAVs have sufficient energy to fulfill their long-term mission, which would otherwise be impossible. The paper provides a detailed description of the mission planner and all of its components. The functionality of the planner is successfully demonstrated in simulated multi-UAV multi-station scenarios.

Pedestrian Tracking with Monocular Camera using Unconstrained 3D Motion Model

A first-principle single-object model is proposed for pedestrian tracking. It is assumed that the extent of the moving object can be described via known statistics in 3D, such as pedestrian height. The proposed model thus need not constrain the object motion in 3D to a common ground plane, which is usual in 3D visual tracking applications. A nonlinear filter for this model is implemented using the unscented Kalman filter (UKF) and tested using the publicly available MOT-17 dataset. The proposed solution yields promising results in 3D while maintaining perfect results when projected into the 2D image. Moreover, the estimation error covariance matches the true one. Unlike conventional methods, the introduced model parameters have convenient meaning and can readily be adjusted for a problem.

Hybrid Neural Network Augmented Physics-based Models for Nonlinear Filtering

In this paper we present a hybrid neural network augmented physics-based modeling (APBM) framework for Bayesian nonlinear latent space estimation. The proposed APBM strategy allows for model adaptation when new operation conditions come into play or the physics-based model is insufficient (or incomplete) to properly describe the latent phenomenon. One advantage of the APBMs and our estimation procedure is the capability of maintaining the physical interpretability of estimated states. Furthermore, we propose a constraint filtering approach to control the neural network contributions to the overall model. We also exploit assumed density filtering techniques and cubature integration rules to present a flexible estimation strategy that can easily deal with nonlinear models and high-dimensional latent spaces. Finally, we demonstrate the efficacy of our methodology by leveraging a target tracking scenario with nonlinear and incomplete measurement and acceleration models, respectively.

Improved Calibration of Numerical Integration Error in Sigma-Point Filters

The sigma-point filters, such as the UKF, which exploit numerical quadrature to obtain an additional order of accuracy in the moment transformation step, are popular alternatives to the ubiquitous EKF. The classical quadrature rules used in the sigma-point filters are motivated via polynomial approximation of the integrand, however in the applied context these assumptions cannot always be justified. As a result, quadrature error can introduce bias into estimated moments, for which there is no compensatory mechanism in the classical sigma-point filters. This can lead in turn to estimates and predictions that are poorly calibrated. In this article, we investigate the Bayes-Sard quadrature method in the context of sigma-point filters, which enables uncertainty due to quadrature error to be formalised within a probabilistic model. Our first contribution is to derive the well-known classical quadratures as special cases of the Bayes-Sard quadrature method. Then a general-purpose moment transform is developed and utilised in the design of novel sigma-point filters, so that uncertainty due to quadrature error is explicitly quantified. Numerical experiments on a challenging tracking example with misspecified initial conditions show that the additional uncertainty quantification built into our method leads to better-calibrated state estimates with improved RMSE.

Student-t Process Quadratures for Filtering of Non-Linear Systems with Heavy-Tailed Noise

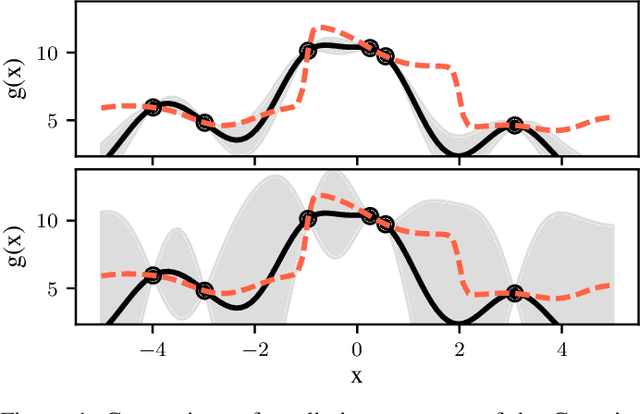
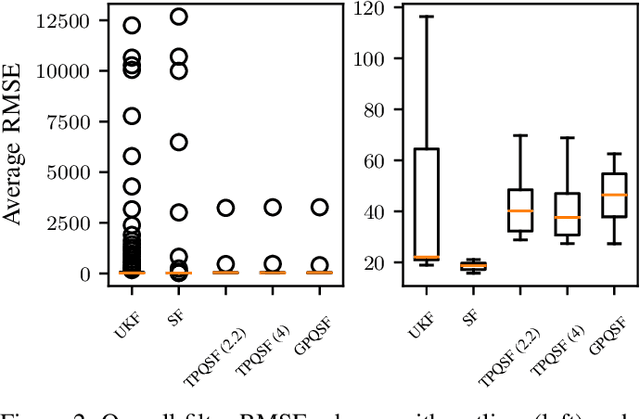
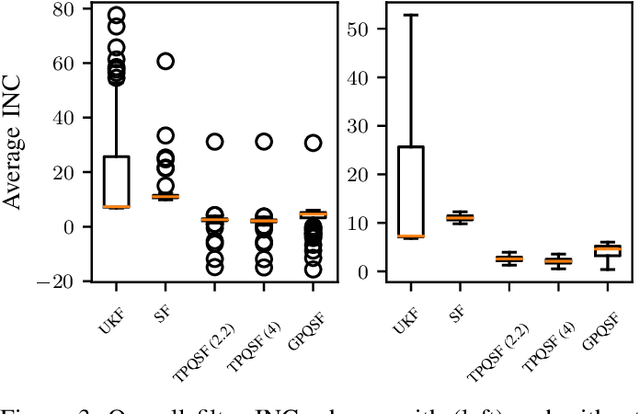
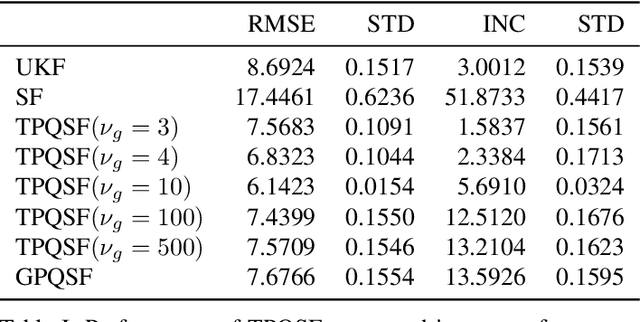
The aim of this article is to design a moment transformation for Student- t distributed random variables, which is able to account for the error in the numerically computed mean. We employ Student-t process quadrature, an instance of Bayesian quadrature, which allows us to treat the integral itself as a random variable whose variance provides information about the incurred integration error. Advantage of the Student- t process quadrature over the traditional Gaussian process quadrature, is that the integral variance depends also on the function values, allowing for a more robust modelling of the integration error. The moment transform is applied in nonlinear sigma-point filtering and evaluated on two numerical examples, where it is shown to outperform the state-of-the-art moment transforms.

Gaussian Process Quadrature Moment Transform

Computation of moments of transformed random variables is a problem appearing in many engineering applications. The current methods for moment transformation are mostly based on the classical quadrature rules which cannot account for the approximation errors. Our aim is to design a method for moment transformation for Gaussian random variables which accounts for the error in the numerically computed mean. We employ an instance of Bayesian quadrature, called Gaussian process quadrature (GPQ), which allows us to treat the integral itself as a random variable, where the integral variance informs about the incurred integration error. Experiments on the coordinate transformation and nonlinear filtering examples show that the proposed GPQ moment transform performs better than the classical transforms.