Guarantees of a Preconditioned Subgradient Algorithm for Overparameterized Asymmetric Low-rank Matrix Recovery
Paper and Code
Oct 22, 2024
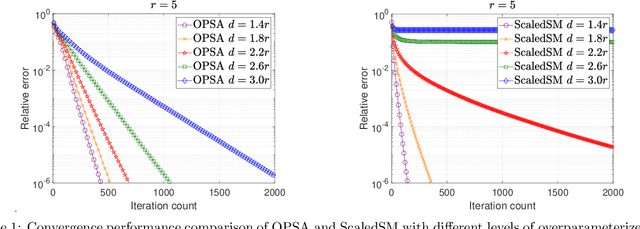
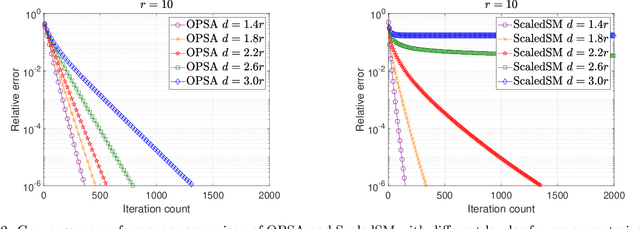
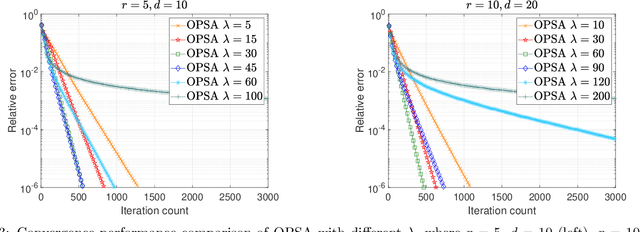
In this paper, we focus on a matrix factorization-based approach for robust low-rank and asymmetric matrix recovery from corrupted measurements. We address the challenging scenario where the rank of the sought matrix is unknown and employ an overparameterized approach using the variational form of the nuclear norm as a regularizer. We propose a subgradient algorithm that inherits the merits of preconditioned algorithms, whose rate of convergence does not depend on the condition number of the sought matrix, and addresses their current limitation, i.e., the lack of convergence guarantees in the case of asymmetric matrices with unknown rank. In this setting, we provide, for the first time in the literature, linear convergence guarantees for the derived overparameterized preconditioned subgradient algorithm in the presence of gross corruptions. Additionally, by applying our approach to matrix sensing, we highlight its merits when the measurement operator satisfies the mixed-norm restricted isometry properties. Lastly, we present numerical experiments that validate our theoretical results and demonstrate the effectiveness of our approach.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge