Generating Origin-Destination Matrices in Neural Spatial Interaction Models
Paper and Code
Oct 09, 2024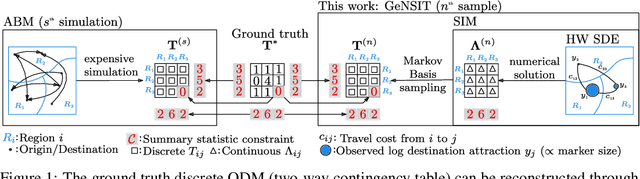


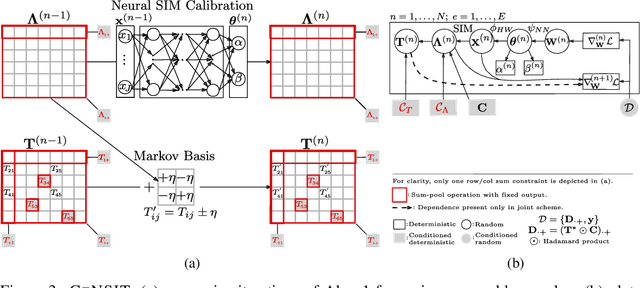
Agent-based models (ABMs) are proliferating as decision-making tools across policy areas in transportation, economics, and epidemiology. In these models, a central object of interest is the discrete origin-destination matrix which captures spatial interactions and agent trip counts between locations. Existing approaches resort to continuous approximations of this matrix and subsequent ad-hoc discretisations in order to perform ABM simulation and calibration. This impedes conditioning on partially observed summary statistics, fails to explore the multimodal matrix distribution over a discrete combinatorial support, and incurs discretisation errors. To address these challenges, we introduce a computationally efficient framework that scales linearly with the number of origin-destination pairs, operates directly on the discrete combinatorial space, and learns the agents' trip intensity through a neural differential equation that embeds spatial interactions. Our approach outperforms the prior art in terms of reconstruction error and ground truth matrix coverage, at a fraction of the computational cost. We demonstrate these benefits in large-scale spatial mobility ABMs in Cambridge, UK and Washington, DC, USA.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge