Scalable Expectation Estimation with Subtractive Mixture Models

Many Monte Carlo (MC) and importance sampling (IS) methods use mixture models (MMs) for their simplicity and ability to capture multimodal distributions. Recently, subtractive mixture models (SMMs), i.e. MMs with negative coefficients, have shown greater expressiveness and success in generative modeling. However, their negative parameters complicate sampling, requiring costly auto-regressive techniques or accept-reject algorithms that do not scale in high dimensions. In this work, we use the difference representation of SMMs to construct an unbiased IS estimator ($\Delta\text{Ex}$) that removes the need to sample from the SMM, enabling high-dimensional expectation estimation with SMMs. In our experiments, we show that $\Delta\text{Ex}$ can achieve comparable estimation quality to auto-regressive sampling while being considerably faster in MC estimation. Moreover, we conduct initial experiments with $\Delta\text{Ex}$ using hand-crafted proposals, gaining first insights into how to construct safe proposals for $\Delta\text{Ex}$.

Causal Optimal Transport of Abstractions

Causal abstraction (CA) theory establishes formal criteria for relating multiple structural causal models (SCMs) at different levels of granularity by defining maps between them. These maps have significant relevance for real-world challenges such as synthesizing causal evidence from multiple experimental environments, learning causally consistent representations at different resolutions, and linking interventions across multiple SCMs. In this work, we propose COTA, the first method to learn abstraction maps from observational and interventional data without assuming complete knowledge of the underlying SCMs. In particular, we introduce a multi-marginal Optimal Transport (OT) formulation that enforces do-calculus causal constraints, together with a cost function that relies on interventional information. We extensively evaluate COTA on synthetic and real world problems, and showcase its advantages over non-causal, independent and aggregated COTA formulations. Finally, we demonstrate the efficiency of our method as a data augmentation tool by comparing it against the state-of-the-art CA learning framework, which assumes fully specified SCMs, on a real-world downstream task.

Adaptive importance sampling for heavy-tailed distributions via $α$-divergence minimization

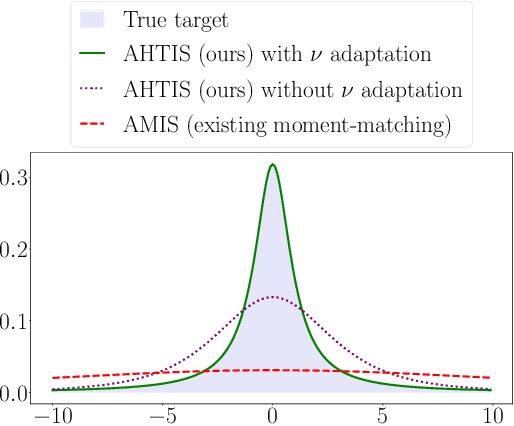
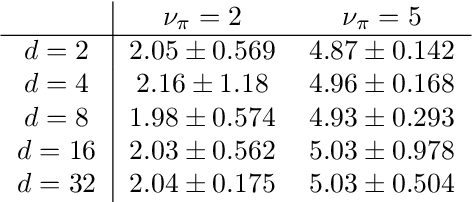
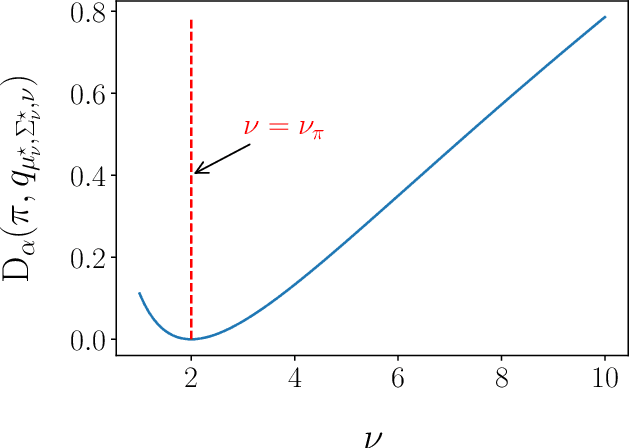
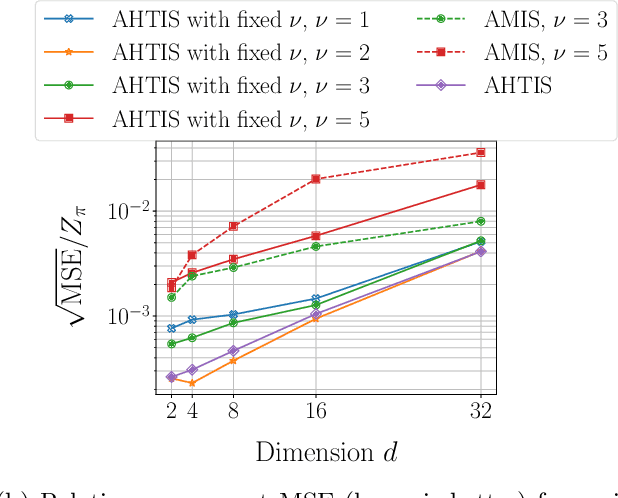
Adaptive importance sampling (AIS) algorithms are widely used to approximate expectations with respect to complicated target probability distributions. When the target has heavy tails, existing AIS algorithms can provide inconsistent estimators or exhibit slow convergence, as they often neglect the target's tail behaviour. To avoid this pitfall, we propose an AIS algorithm that approximates the target by Student-t proposal distributions. We adapt location and scale parameters by matching the escort moments - which are defined even for heavy-tailed distributions - of the target and the proposal. These updates minimize the $\alpha$-divergence between the target and the proposal, thereby connecting with variational inference. We then show that the $\alpha$-divergence can be approximated by a generalized notion of effective sample size and leverage this new perspective to adapt the tail parameter with Bayesian optimization. We demonstrate the efficacy of our approach through applications to synthetic targets and a Bayesian Student-t regression task on a real example with clinical trial data.

Causal Entropy Optimization

We study the problem of globally optimizing the causal effect on a target variable of an unknown causal graph in which interventions can be performed. This problem arises in many areas of science including biology, operations research and healthcare. We propose Causal Entropy Optimization (CEO), a framework that generalizes Causal Bayesian Optimization (CBO) to account for all sources of uncertainty, including the one arising from the causal graph structure. CEO incorporates the causal structure uncertainty both in the surrogate models for the causal effects and in the mechanism used to select interventions via an information-theoretic acquisition function. The resulting algorithm automatically trades-off structure learning and causal effect optimization, while naturally accounting for observation noise. For various synthetic and real-world structural causal models, CEO achieves faster convergence to the global optimum compared with CBO while also learning the graph. Furthermore, our joint approach to structure learning and causal optimization improves upon sequential, structure-learning-first approaches.