Towards Expressive Priors for Bayesian Neural Networks: Poisson Process Radial Basis Function Networks

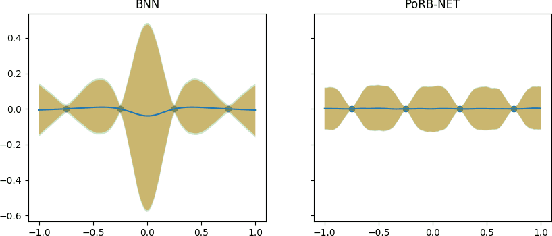
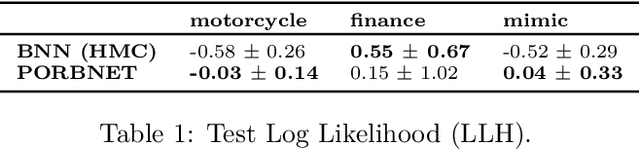
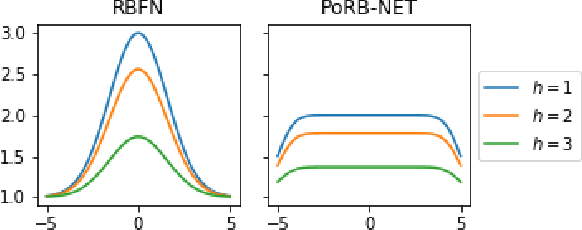
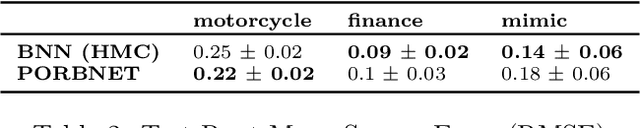
While Bayesian neural networks have many appealing characteristics, current priors do not easily allow users to specify basic properties such as expected lengthscale or amplitude variance. In this work, we introduce Poisson Process Radial Basis Function Networks, a novel prior that is able to encode amplitude stationarity and input-dependent lengthscale. We prove that our novel formulation allows for a decoupled specification of these properties, and that the estimated regression function is consistent as the number of observations tends to infinity. We demonstrate its behavior on synthetic and real examples.