Fixing Variational Bayes: Deterministic Variational Inference for Bayesian Neural Networks

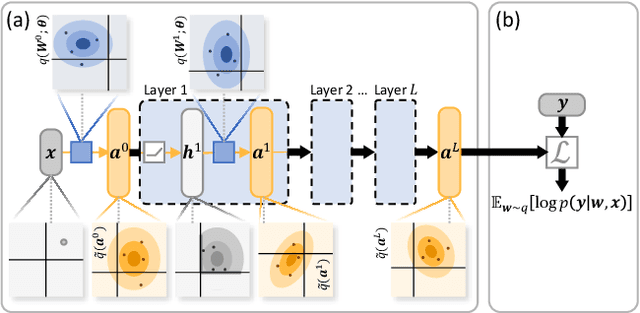
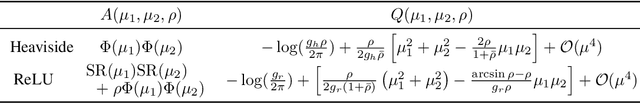
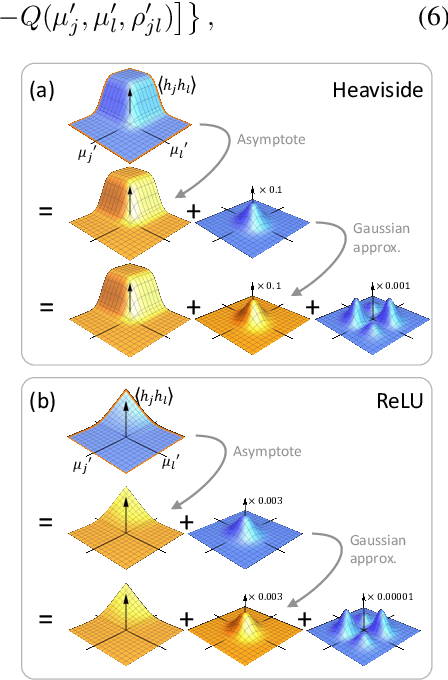
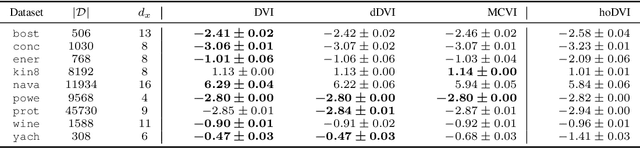
Bayesian neural networks (BNNs) hold great promise as a flexible and principled solution to deal with uncertainty when learning from finite data. Among approaches to realize probabilistic inference in deep neural networks, variational Bayes (VB) is theoretically grounded, generally applicable, and computationally efficient. With wide recognition of potential advantages, why is it that variational Bayes has seen very limited practical use for BNNs in real applications? We argue that variational inference in neural networks is fragile: successful implementations require careful initialization and tuning of prior variances, as well as controlling the variance of Monte Carlo gradient estimates. We fix VB and turn it into a robust inference tool for Bayesian neural networks. We achieve this with two innovations: first, we introduce a novel deterministic method to approximate moments in neural networks, eliminating gradient variance; second, we introduce a hierarchical prior for parameters and a novel empirical Bayes procedure for automatically selecting prior variances. Combining these two innovations, the resulting method is highly efficient and robust. On the application of heteroscedastic regression we demonstrate strong predictive performance over alternative approaches.