A machine learning accelerated inverse design of underwater acoustic polyurethane coatings with cylindrical voids

Here, we report the development of a detailed "Materials Informatics" framework for the design of acoustic coatings for underwater sound attenuation through integrating Machine Learning (ML) and statistical optimization algorithms with a Finite Element Model (FEM). The finite element models were developed to simulate the realistic performance of the acoustic coatings based on polyurethane (PU) elastomers with embedded cylindrical voids. The FEM results revealed that the frequency-dependent viscoelastic behavior of the polyurethane matrix has a significant impact on the magnitude and frequency of the absorption peak associated with the cylinders at low frequencies, which has been commonly ignored in previous studies on similar systems. The data generated from the FEM was used to train a Deep Neural Network (DNN) to accelerate the design process, and subsequently, was integrated with a Genetic Algorithm (GA) to determine the optimal geometric parameters of the cylinders to achieve maximized, broadband, low-frequency waterborne sound attenuation. A significant, broadband, low-frequency attenuation is achieved by optimally configuring the layers of cylindrical voids and using attenuation mechanisms, including Fabry-P\'erot resonance and Bragg scattering of the layers of voids. Integration of the machine learning technique into the optimization algorithm further accelerated the exploration of the high dimensional design space for the targeted performance. The developed DNN exhibited significantly increased speed (by a factor of $4.5\times 10^3$ ) in predicting the absorption coefficient compared to the conventional FEM(s). Therefore, the acceleration brought by the materials informatics framework brings a paradigm shift to the design and development of acoustic coatings compared to the conventional trial-and-error practices.

Efficient Amortised Bayesian Inference for Hierarchical and Nonlinear Dynamical Systems

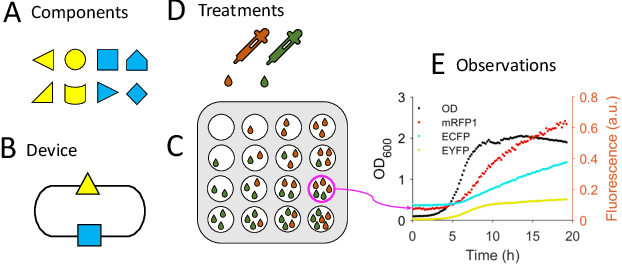
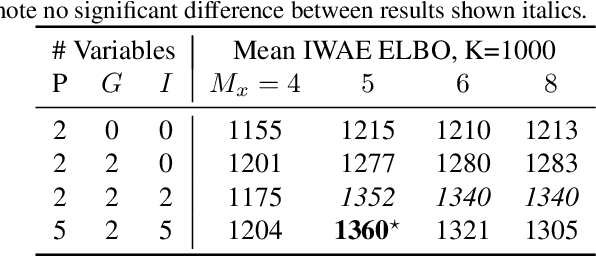
We introduce a flexible, scalable Bayesian inference framework for nonlinear dynamical systems characterised by distinct and hierarchical variability at the individual, group, and population levels. Our model class is a generalisation of nonlinear mixed-effects (NLME) dynamical systems, the statistical workhorse for many experimental sciences. We cast parameter inference as stochastic optimisation of an end-to-end differentiable, block-conditional variational autoencoder. We specify the dynamics of the data-generating process as an ordinary differential equation (ODE) such that both the ODE and its solver are fully differentiable. This model class is highly flexible: the ODE right-hand sides can be a mixture of user-prescribed or "white-box" sub-components and neural network or "black-box" sub-components. Using stochastic optimisation, our amortised inference algorithm could seamlessly scale up to massive data collection pipelines (common in labs with robotic automation). Finally, our framework supports interpretability with respect to the underlying dynamics, as well as predictive generalization to unseen combinations of group components (also called "zero-shot" learning). We empirically validate our method by predicting the dynamic behaviour of bacteria that were genetically engineered to function as biosensors.