Sum-of-squares lower bounds for Non-Gaussian Component Analysis

Non-Gaussian Component Analysis (NGCA) is the statistical task of finding a non-Gaussian direction in a high-dimensional dataset. Specifically, given i.i.d.\ samples from a distribution $P^A_{v}$ on $\mathbb{R}^n$ that behaves like a known distribution $A$ in a hidden direction $v$ and like a standard Gaussian in the orthogonal complement, the goal is to approximate the hidden direction. The standard formulation posits that the first $k-1$ moments of $A$ match those of the standard Gaussian and the $k$-th moment differs. Under mild assumptions, this problem has sample complexity $O(n)$. On the other hand, all known efficient algorithms require $\Omega(n^{k/2})$ samples. Prior work developed sharp Statistical Query and low-degree testing lower bounds suggesting an information-computation tradeoff for this problem. Here we study the complexity of NGCA in the Sum-of-Squares (SoS) framework. Our main contribution is the first super-constant degree SoS lower bound for NGCA. Specifically, we show that if the non-Gaussian distribution $A$ matches the first $(k-1)$ moments of $\mathcal{N}(0, 1)$ and satisfies other mild conditions, then with fewer than $n^{(1 - \varepsilon)k/2}$ many samples from the normal distribution, with high probability, degree $(\log n)^{{1\over 2}-o_n(1)}$ SoS fails to refute the existence of such a direction $v$. Our result significantly strengthens prior work by establishing a super-polynomial information-computation tradeoff against a broader family of algorithms. As corollaries, we obtain SoS lower bounds for several problems in robust statistics and the learning of mixture models. Our SoS lower bound proof introduces a novel technique, that we believe may be of broader interest, and a number of refinements over existing methods.

Exact nuclear norm, completion and decomposition for random overcomplete tensors via degree-4 SOS

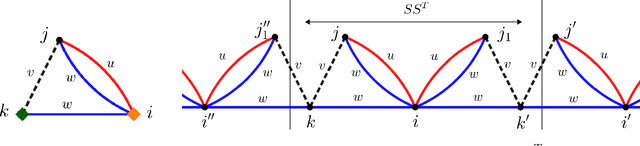
In this paper we show that simple semidefinite programs inspired by degree $4$ SOS can exactly solve the tensor nuclear norm, tensor decomposition, and tensor completion problems on tensors with random asymmetric components. More precisely, for tensor nuclear norm and tensor decomposition, we show that w.h.p. these semidefinite programs can exactly find the nuclear norm and components of an $(n\times n\times n)$-tensor $\mathcal{T}$ with $m\leq n^{3/2}/polylog(n)$ random asymmetric components. For tensor completion, we show that w.h.p. the semidefinite program introduced by Potechin \& Steurer (2017) can exactly recover an $(n\times n\times n)$-tensor $\mathcal{T}$ with $m$ random asymmetric components from only $n^{3/2}m\, polylog(n)$ randomly observed entries. This gives the first theoretical guarantees for exact tensor completion in the overcomplete regime. This matches the best known results for approximate versions of these problems given by Barak \& Moitra (2015) for tensor completion, and Ma, Shi \& Steurer (2016) for tensor decomposition.

Exact tensor completion with sum-of-squares

We obtain the first polynomial-time algorithm for exact tensor completion that improves over the bound implied by reduction to matrix completion. The algorithm recovers an unknown 3-tensor with $r$ incoherent, orthogonal components in $\mathbb R^n$ from $r\cdot \tilde O(n^{1.5})$ randomly observed entries of the tensor. This bound improves over the previous best one of $r\cdot \tilde O(n^{2})$ by reduction to exact matrix completion. Our bound also matches the best known results for the easier problem of approximate tensor completion (Barak & Moitra, 2015). Our algorithm and analysis extends seminal results for exact matrix completion (Candes & Recht, 2009) to the tensor setting via the sum-of-squares method. The main technical challenge is to show that a small number of randomly chosen monomials are enough to construct a degree-3 polynomial with precisely planted orthogonal global optima over the sphere and that this fact can be certified within the sum-of-squares proof system.