Learning a Single Neuron Robustly to Distributional Shifts and Adversarial Label Noise

We study the problem of learning a single neuron with respect to the $L_2^2$-loss in the presence of adversarial distribution shifts, where the labels can be arbitrary, and the goal is to find a ``best-fit'' function. More precisely, given training samples from a reference distribution $\mathcal{p}_0$, the goal is to approximate the vector $\mathbf{w}^*$ which minimizes the squared loss with respect to the worst-case distribution that is close in $\chi^2$-divergence to $\mathcal{p}_{0}$. We design a computationally efficient algorithm that recovers a vector $ \hat{\mathbf{w}}$ satisfying $\mathbb{E}_{\mathcal{p}^*} (\sigma(\hat{\mathbf{w}} \cdot \mathbf{x}) - y)^2 \leq C \, \mathbb{E}_{\mathcal{p}^*} (\sigma(\mathbf{w}^* \cdot \mathbf{x}) - y)^2 + \epsilon$, where $C>1$ is a dimension-independent constant and $(\mathbf{w}^*, \mathcal{p}^*)$ is the witness attaining the min-max risk $\min_{\mathbf{w}~:~\|\mathbf{w}\| \leq W} \max_{\mathcal{p}} \mathbb{E}_{(\mathbf{x}, y) \sim \mathcal{p}} (\sigma(\mathbf{w} \cdot \mathbf{x}) - y)^2 - \nu \chi^2(\mathcal{p}, \mathcal{p}_0)$. Our algorithm follows a primal-dual framework and is designed by directly bounding the risk with respect to the original, nonconvex $L_2^2$ loss. From an optimization standpoint, our work opens new avenues for the design of primal-dual algorithms under structured nonconvexity.

Robust Second-Order Nonconvex Optimization and Its Application to Low Rank Matrix Sensing

Finding an approximate second-order stationary point (SOSP) is a well-studied and fundamental problem in stochastic nonconvex optimization with many applications in machine learning. However, this problem is poorly understood in the presence of outliers, limiting the use of existing nonconvex algorithms in adversarial settings. In this paper, we study the problem of finding SOSPs in the strong contamination model, where a constant fraction of datapoints are arbitrarily corrupted. We introduce a general framework for efficiently finding an approximate SOSP with \emph{dimension-independent} accuracy guarantees, using $\widetilde{O}({D^2}/{\epsilon})$ samples where $D$ is the ambient dimension and $\epsilon$ is the fraction of corrupted datapoints. As a concrete application of our framework, we apply it to the problem of low rank matrix sensing, developing efficient and provably robust algorithms that can tolerate corruptions in both the sensing matrices and the measurements. In addition, we establish a Statistical Query lower bound providing evidence that the quadratic dependence on $D$ in the sample complexity is necessary for computationally efficient algorithms.

DAIL: Data Augmentation for In-Context Learning via Self-Paraphrase

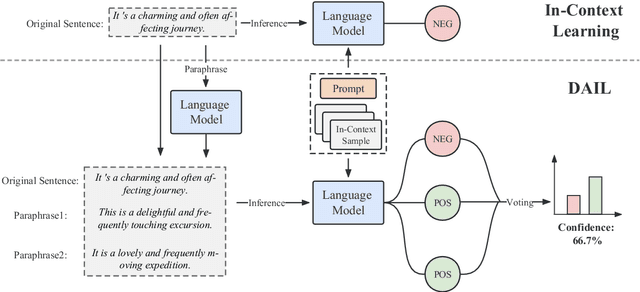
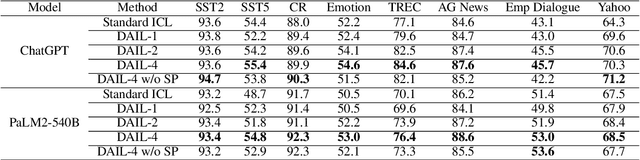
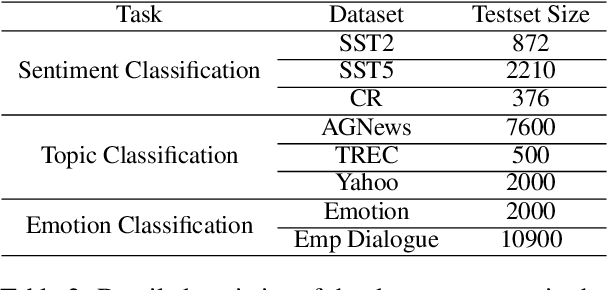
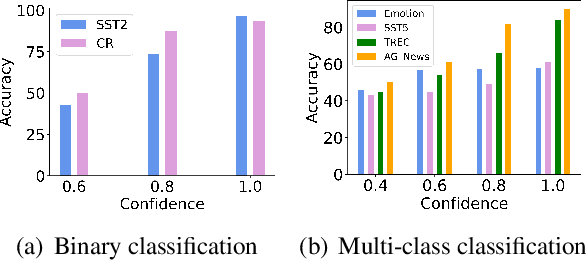
In-Context Learning (ICL) combined with pre-trained large language models has achieved promising results on various NLP tasks. However, ICL requires high-quality annotated demonstrations which might not be available in real-world scenarios. To overcome this limitation, we propose \textbf{D}ata \textbf{A}ugmentation for \textbf{I}n-Context \textbf{L}earning (\textbf{DAIL}). DAIL leverages the intuition that large language models are more familiar with the content generated by themselves. It first utilizes the language model to generate paraphrases of the test sample and employs majority voting to determine the final result based on individual predictions. Our extensive empirical evaluation shows that DAIL outperforms the standard ICL method and other ensemble-based methods in the low-resource scenario. Additionally, we explore the use of voting consistency as a confidence score of the model when the logits of predictions are inaccessible. We believe our work will stimulate further research on ICL in low-resource settings.

A randomized algorithm for nonconvex minimization with inexact evaluations and complexity guarantees

We consider minimization of a smooth nonconvex function with inexact oracle access to gradient and Hessian (but not the function value) to achieve $(\epsilon_{g}, \epsilon_{H})$-approximate second-order optimality. A novel feature of our method is that if an approximate direction of negative curvature is chosen as the step, we choose its sense to be positive or negative with equal probability. We also use relative inexactness measures on gradient and Hessian and relax the coupling between the first- and second-order tolerances $\epsilon_{g}$ and $\epsilon_{H}$. Our convergence analysis includes both an expectation bound based on martingale analysis and a high-probability bound based on concentration inequalities. We apply our algorithm to empirical risk minimization problems and obtain gradient sample complexity.