Lexico: Extreme KV Cache Compression via Sparse Coding over Universal Dictionaries

We introduce Lexico, a novel KV cache compression method that leverages sparse coding with a universal dictionary. Our key finding is that key-value cache in modern LLMs can be accurately approximated using sparse linear combination from a small, input-agnostic dictionary of ~4k atoms, enabling efficient compression across different input prompts, tasks and models. Using orthogonal matching pursuit for sparse approximation, Lexico achieves flexible compression ratios through direct sparsity control. On GSM8K, across multiple model families (Mistral, Llama 3, Qwen2.5), Lexico maintains 90-95% of the original performance while using only 15-25% of the full KV-cache memory, outperforming both quantization and token eviction methods. Notably, Lexico remains effective in low memory regimes where 2-bit quantization fails, achieving up to 1.7x better compression on LongBench and GSM8K while maintaining high accuracy.

Task Diversity Shortens the ICL Plateau

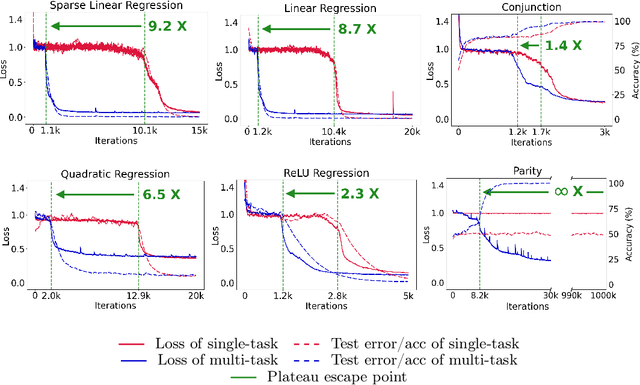
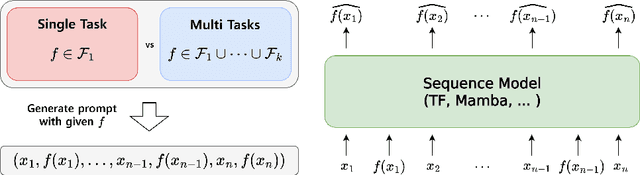
In-context learning (ICL) describes a language model's ability to generate outputs based on a set of input demonstrations and a subsequent query. To understand this remarkable capability, researchers have studied simplified, stylized models. These studies have consistently observed long loss plateaus, during which models exhibit minimal improvement, followed by a sudden, rapid surge of learning. In this work, we reveal that training on multiple diverse ICL tasks simultaneously shortens the loss plateaus, making each task easier to learn. This finding is surprising as it contradicts the natural intuition that the combined complexity of multiple ICL tasks would lengthen the learning process, not shorten it. Our result suggests that the recent success in large-scale training of language models may be attributed not only to the richness of the data at scale but also to the easier optimization (training) induced by the diversity of natural language training data.

Can Mamba Learn How to Learn? A Comparative Study on In-Context Learning Tasks

State-space models (SSMs), such as Mamba Gu & Dao (2034), have been proposed as alternatives to Transformer networks in language modeling, by incorporating gating, convolutions, and input-dependent token selection to mitigate the quadratic cost of multi-head attention. Although SSMs exhibit competitive performance, their in-context learning (ICL) capabilities, a remarkable emergent property of modern language models that enables task execution without parameter optimization, remain underexplored compared to Transformers. In this study, we evaluate the ICL performance of SSMs, focusing on Mamba, against Transformer models across various tasks. Our results show that SSMs perform comparably to Transformers in standard regression ICL tasks, while outperforming them in tasks like sparse parity learning. However, SSMs fall short in tasks involving non-standard retrieval functionality. To address these limitations, we introduce a hybrid model, \variant, that combines Mamba with attention blocks, surpassing individual models in tasks where they struggle independently. Our findings suggest that hybrid architectures offer promising avenues for enhancing ICL in language models.

Balanced Group Convolution: An Improved Group Convolution Based on Approximability Estimates

The performance of neural networks has been significantly improved by increasing the number of channels in convolutional layers. However, this increase in performance comes with a higher computational cost, resulting in numerous studies focused on reducing it. One promising approach to address this issue is group convolution, which effectively reduces the computational cost by grouping channels. However, to the best of our knowledge, there has been no theoretical analysis on how well the group convolution approximates the standard convolution. In this paper, we mathematically analyze the approximation of the group convolution to the standard convolution with respect to the number of groups. Furthermore, we propose a novel variant of the group convolution called balanced group convolution, which shows a higher approximation with a small additional computational cost. We provide experimental results that validate our theoretical findings and demonstrate the superior performance of the balanced group convolution over other variants of group convolution.

Distribution-Independent Regression for Generalized Linear Models with Oblivious Corruptions

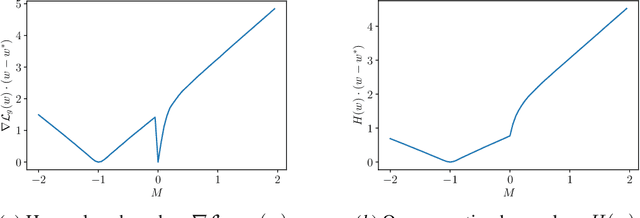
We demonstrate the first algorithms for the problem of regression for generalized linear models (GLMs) in the presence of additive oblivious noise. We assume we have sample access to examples $(x, y)$ where $y$ is a noisy measurement of $g(w^* \cdot x)$. In particular, \new{the noisy labels are of the form} $y = g(w^* \cdot x) + \xi + \epsilon$, where $\xi$ is the oblivious noise drawn independently of $x$ \new{and satisfies} $\Pr[\xi = 0] \geq o(1)$, and $\epsilon \sim \mathcal N(0, \sigma^2)$. Our goal is to accurately recover a \new{parameter vector $w$ such that the} function $g(w \cdot x)$ \new{has} arbitrarily small error when compared to the true values $g(w^* \cdot x)$, rather than the noisy measurements $y$. We present an algorithm that tackles \new{this} problem in its most general distribution-independent setting, where the solution may not \new{even} be identifiable. \new{Our} algorithm returns \new{an accurate estimate of} the solution if it is identifiable, and otherwise returns a small list of candidates, one of which is close to the true solution. Furthermore, we \new{provide} a necessary and sufficient condition for identifiability, which holds in broad settings. \new{Specifically,} the problem is identifiable when the quantile at which $\xi + \epsilon = 0$ is known, or when the family of hypotheses does not contain candidates that are nearly equal to a translated $g(w^* \cdot x) + A$ for some real number $A$, while also having large error when compared to $g(w^* \cdot x)$. This is the first \new{algorithmic} result for GLM regression \new{with oblivious noise} which can handle more than half the samples being arbitrarily corrupted. Prior work focused largely on the setting of linear regression, and gave algorithms under restrictive assumptions.

DualFL: A Duality-based Federated Learning Algorithm with Communication Acceleration in the General Convex Regime

We propose a novel training algorithm called DualFL (Dualized Federated Learning), for solving a distributed optimization problem in federated learning. Our approach is based on a specific dual formulation of the federated learning problem. DualFL achieves communication acceleration under various settings on smoothness and strong convexity of the problem. Moreover, it theoretically guarantees the use of inexact local solvers, preserving its optimal communication complexity even with inexact local solutions. DualFL is the first federated learning algorithm that achieves communication acceleration, even when the cost function is either nonsmooth or non-strongly convex. Numerical results demonstrate that the practical performance of DualFL is comparable to those of state-of-the-art federated learning algorithms, and it is robust with respect to hyperparameter tuning.

Prompted LLMs as Chatbot Modules for Long Open-domain Conversation

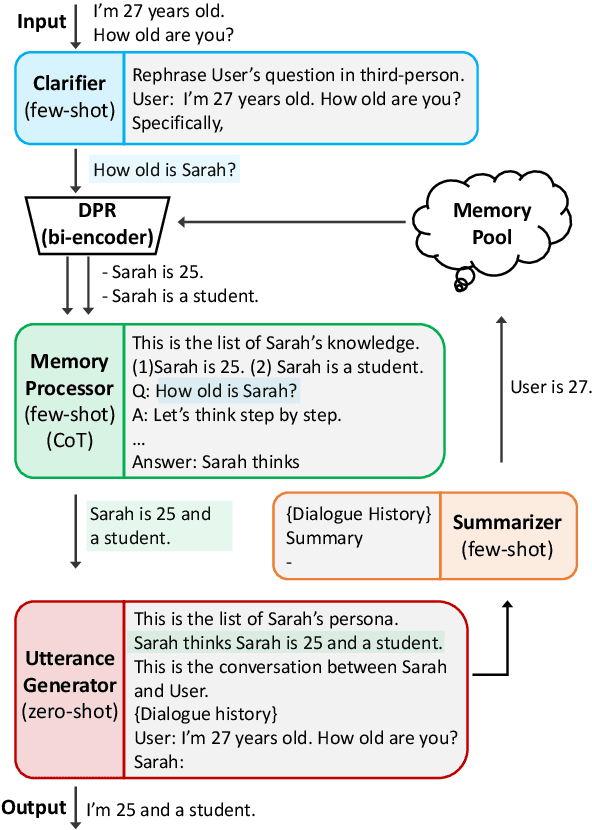
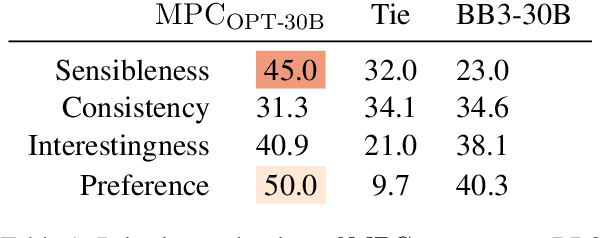
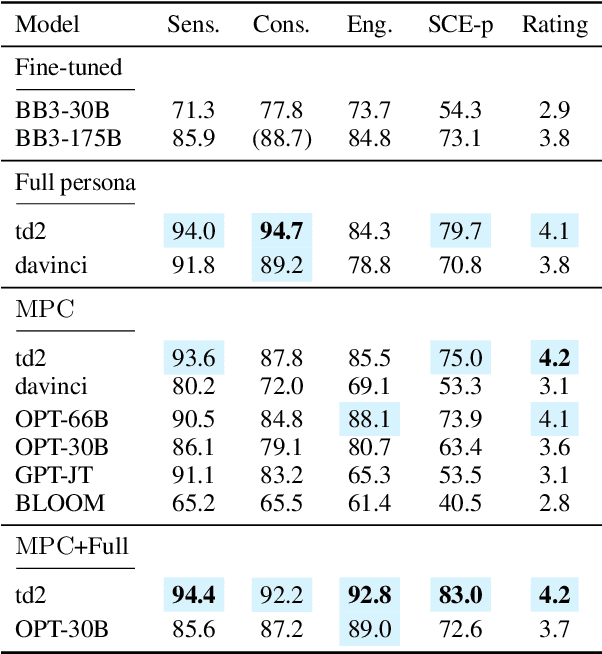
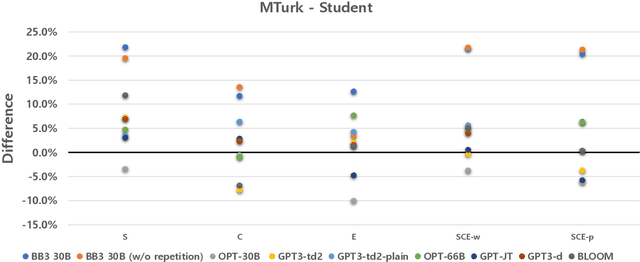
In this paper, we propose MPC (Modular Prompted Chatbot), a new approach for creating high-quality conversational agents without the need for fine-tuning. Our method utilizes pre-trained large language models (LLMs) as individual modules for long-term consistency and flexibility, by using techniques such as few-shot prompting, chain-of-thought (CoT), and external memory. Our human evaluation results show that MPC is on par with fine-tuned chatbot models in open-domain conversations, making it an effective solution for creating consistent and engaging chatbots.

Two-level Group Convolution

Group convolution has been widely used in order to reduce the computation time of convolution, which takes most of the training time of convolutional neural networks. However, it is well known that a large number of groups significantly reduce the performance of group convolution. In this paper, we propose a new convolution methodology called ``two-level'' group convolution that is robust with respect to the increase of the number of groups and suitable for multi-GPU parallel computation. We first observe that the group convolution can be interpreted as a one-level block Jacobi approximation of the standard convolution, which is a popular notion in the field of numerical analysis. In numerical analysis, there have been numerous studies on the two-level method that introduces an intergroup structure that resolves the performance degradation issue without disturbing parallel computation. Motivated by these, we introduce a coarse-level structure which promotes intergroup communication without being a bottleneck in the group convolution. We show that all the additional work induced by the coarse-level structure can be efficiently processed in a distributed memory system. Numerical results that verify the robustness of the proposed method with respect to the number of groups are presented. Moreover, we compare the proposed method to various approaches for group convolution in order to highlight the superiority of the proposed method in terms of execution time, memory efficiency, and performance.

ReLU Regression with Massart Noise

We study the fundamental problem of ReLU regression, where the goal is to fit Rectified Linear Units (ReLUs) to data. This supervised learning task is efficiently solvable in the realizable setting, but is known to be computationally hard with adversarial label noise. In this work, we focus on ReLU regression in the Massart noise model, a natural and well-studied semi-random noise model. In this model, the label of every point is generated according to a function in the class, but an adversary is allowed to change this value arbitrarily with some probability, which is {\em at most} $\eta < 1/2$. We develop an efficient algorithm that achieves exact parameter recovery in this model under mild anti-concentration assumptions on the underlying distribution. Such assumptions are necessary for exact recovery to be information-theoretically possible. We demonstrate that our algorithm significantly outperforms naive applications of $\ell_1$ and $\ell_2$ regression on both synthetic and real data.

Parareal Neural Networks Emulating a Parallel-in-time Algorithm

As deep neural networks (DNNs) become deeper, the training time increases. In this perspective, multi-GPU parallel computing has become a key tool in accelerating the training of DNNs. In this paper, we introduce a novel methodology to construct a parallel neural network that can utilize multiple GPUs simultaneously from a given DNN. We observe that layers of DNN can be interpreted as the time step of a time-dependent problem and can be parallelized by emulating a parallel-in-time algorithm called parareal. The parareal algorithm consists of fine structures which can be implemented in parallel and a coarse structure which gives suitable approximations to the fine structures. By emulating it, the layers of DNN are torn to form a parallel structure which is connected using a suitable coarse network. We report accelerated and accuracy-preserved results of the proposed methodology applied to VGG-16 and ResNet-1001 on several datasets.