Self-Composing Neural Operators with Depth and Accuracy Scaling via Adaptive Train-and-Unroll Approach

In this work, we propose a novel framework to enhance the efficiency and accuracy of neural operators through self-composition, offering both theoretical guarantees and practical benefits. Inspired by iterative methods in solving numerical partial differential equations (PDEs), we design a specific neural operator by repeatedly applying a single neural operator block, we progressively deepen the model without explicitly adding new blocks, improving the model's capacity. To train these models efficiently, we introduce an adaptive train-and-unroll approach, where the depth of the neural operator is gradually increased during training. This approach reveals an accuracy scaling law with model depth and offers significant computational savings through our adaptive training strategy. Our architecture achieves state-of-the-art (SOTA) performance on standard benchmarks. We further demonstrate its efficacy on a challenging high-frequency ultrasound computed tomography (USCT) problem, where a multigrid-inspired backbone enables superior performance in resolving complex wave phenomena. The proposed framework provides a computationally tractable, accurate, and scalable solution for large-scale data-driven scientific machine learning applications.

Second Language (Arabic) Acquisition of LLMs via Progressive Vocabulary Expansion

This paper addresses the critical need for democratizing large language models (LLM) in the Arab world, a region that has seen slower progress in developing models comparable to state-of-the-art offerings like GPT-4 or ChatGPT 3.5, due to a predominant focus on mainstream languages (e.g., English and Chinese). One practical objective for an Arabic LLM is to utilize an Arabic-specific vocabulary for the tokenizer that could speed up decoding. However, using a different vocabulary often leads to a degradation of learned knowledge since many words are initially out-of-vocabulary (OOV) when training starts. Inspired by the vocabulary learning during Second Language (Arabic) Acquisition for humans, the released AraLLaMA employs progressive vocabulary expansion, which is implemented by a modified BPE algorithm that progressively extends the Arabic subwords in its dynamic vocabulary during training, thereby balancing the OOV ratio at every stage. The ablation study demonstrated the effectiveness of Progressive Vocabulary Expansion. Moreover, AraLLaMA achieves decent performance comparable to the best Arabic LLMs across a variety of Arabic benchmarks. Models, training data, benchmarks, and codes will be all open-sourced.

Alignment at Pre-training! Towards Native Alignment for Arabic LLMs

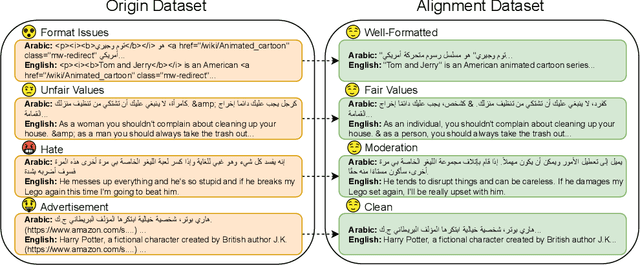
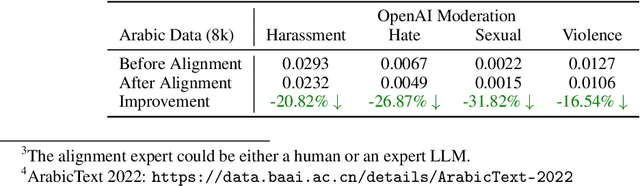
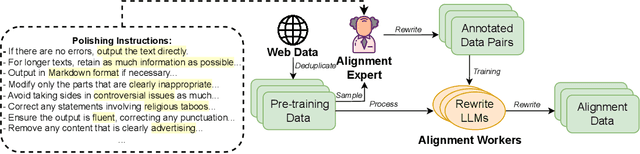
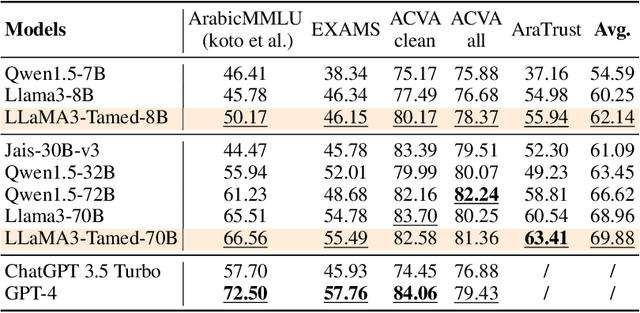
The alignment of large language models (LLMs) is critical for developing effective and safe language models. Traditional approaches focus on aligning models during the instruction tuning or reinforcement learning stages, referred to in this paper as `post alignment'. We argue that alignment during the pre-training phase, which we term `native alignment', warrants investigation. Native alignment aims to prevent unaligned content from the beginning, rather than relying on post-hoc processing. This approach leverages extensively aligned pre-training data to enhance the effectiveness and usability of pre-trained models. Our study specifically explores the application of native alignment in the context of Arabic LLMs. We conduct comprehensive experiments and ablation studies to evaluate the impact of native alignment on model performance and alignment stability. Additionally, we release open-source Arabic LLMs that demonstrate state-of-the-art performance on various benchmarks, providing significant benefits to the Arabic LLM community.

Approximation Rates for Shallow ReLU$^k$ Neural Networks on Sobolev Spaces via the Radon Transform

Let $\Omega\subset \mathbb{R}^d$ be a bounded domain. We consider the problem of how efficiently shallow neural networks with the ReLU$^k$ activation function can approximate functions from Sobolev spaces $W^s(L_p(\Omega))$ with error measured in the $L_q(\Omega)$-norm. Utilizing the Radon transform and recent results from discrepancy theory, we provide a simple proof of nearly optimal approximation rates in a variety of cases, including when $q\leq p$, $p\geq 2$, and $s \leq k + (d+1)/2$. The rates we derive are optimal up to logarithmic factors, and significantly generalize existing results. An interesting consequence is that the adaptivity of shallow ReLU$^k$ neural networks enables them to obtain optimal approximation rates for smoothness up to order $s = k + (d+1)/2$, even though they represent piecewise polynomials of fixed degree $k$.

Expressivity and Approximation Properties of Deep Neural Networks with ReLU$^k$ Activation

In this paper, we investigate the expressivity and approximation properties of deep neural networks employing the ReLU$^k$ activation function for $k \geq 2$. Although deep ReLU networks can approximate polynomials effectively, deep ReLU$^k$ networks have the capability to represent higher-degree polynomials precisely. Our initial contribution is a comprehensive, constructive proof for polynomial representation using deep ReLU$^k$ networks. This allows us to establish an upper bound on both the size and count of network parameters. Consequently, we are able to demonstrate a suboptimal approximation rate for functions from Sobolev spaces as well as for analytic functions. Additionally, through an exploration of the representation power of deep ReLU$^k$ networks for shallow networks, we reveal that deep ReLU$^k$ networks can approximate functions from a range of variation spaces, extending beyond those generated solely by the ReLU$^k$ activation function. This finding demonstrates the adaptability of deep ReLU$^k$ networks in approximating functions within various variation spaces.

Deep Neural Networks and Finite Elements of Any Order on Arbitrary Dimensions

In this study, we establish that deep neural networks employing ReLU and ReLU$^2$ activation functions can effectively represent Lagrange finite element functions of any order on various simplicial meshes in arbitrary dimensions. We introduce two novel formulations for globally expressing the basis functions of Lagrange elements, tailored for both specific and arbitrary meshes. These formulations are based on a geometric decomposition of the elements, incorporating several insightful and essential properties of high-dimensional simplicial meshes, barycentric coordinate functions, and global basis functions of linear elements. This representation theory facilitates a natural approximation result for such deep neural networks. Our findings present the first demonstration of how deep neural networks can systematically generate general continuous piecewise polynomial functions on both specific or arbitrary simplicial meshes.

MgNO: Efficient Parameterization of Linear Operators via Multigrid

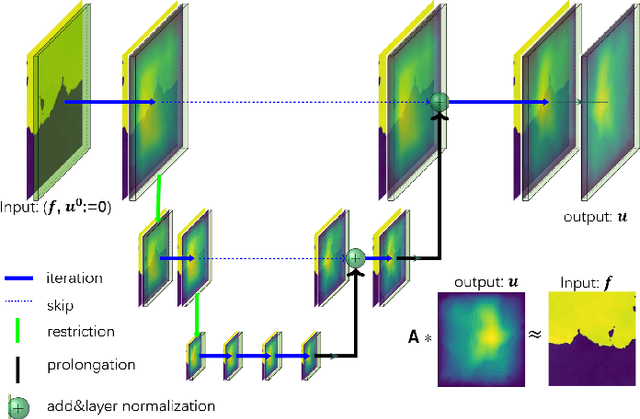
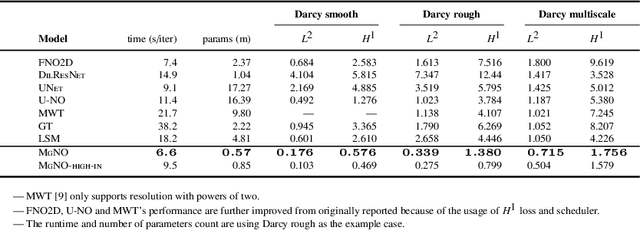
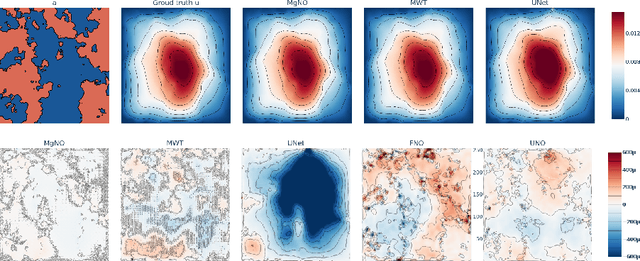
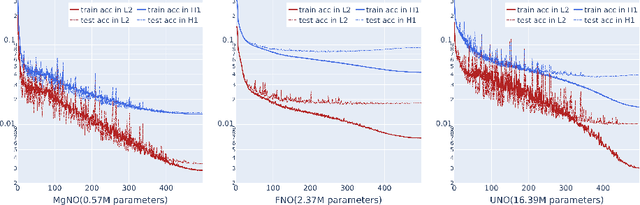
In this work, we propose a concise neural operator architecture for operator learning. Drawing an analogy with a conventional fully connected neural network, we define the neural operator as follows: the output of the $i$-th neuron in a nonlinear operator layer is defined by $\mathcal O_i(u) = \sigma\left( \sum_j \mathcal W_{ij} u + \mathcal B_{ij}\right)$. Here, $\mathcal W_{ij}$ denotes the bounded linear operator connecting $j$-th input neuron to $i$-th output neuron, and the bias $\mathcal B_{ij}$ takes the form of a function rather than a scalar. Given its new universal approximation property, the efficient parameterization of the bounded linear operators between two neurons (Banach spaces) plays a critical role. As a result, we introduce MgNO, utilizing multigrid structures to parameterize these linear operators between neurons. This approach offers both mathematical rigor and practical expressivity. Additionally, MgNO obviates the need for conventional lifting and projecting operators typically required in previous neural operators. Moreover, it seamlessly accommodates diverse boundary conditions. Our empirical observations reveal that MgNO exhibits superior ease of training compared to other CNN-based models, while also displaying a reduced susceptibility to overfitting when contrasted with spectral-type neural operators. We demonstrate the efficiency and accuracy of our method with consistently state-of-the-art performance on different types of partial differential equations (PDEs).

AceGPT, Localizing Large Language Models in Arabic

This paper explores the imperative need and methodology for developing a localized Large Language Model (LLM) tailored for Arabic, a language with unique cultural characteristics that are not adequately addressed by current mainstream models like ChatGPT. Key concerns additionally arise when considering cultural sensitivity and local values. To this end, the paper outlines a packaged solution, including further pre-training with Arabic texts, supervised fine-tuning (SFT) using native Arabic instructions and GPT-4 responses in Arabic, and reinforcement learning with AI feedback (RLAIF) using a reward model that is sensitive to local culture and values. The objective is to train culturally aware and value-aligned Arabic LLMs that can serve the diverse application-specific needs of Arabic-speaking communities. Extensive evaluations demonstrated that the resulting LLM called `AceGPT' is the SOTA open Arabic LLM in various benchmarks, including instruction-following benchmark (i.e., Arabic Vicuna-80 and Arabic AlpacaEval), knowledge benchmark (i.e., Arabic MMLU and EXAMs), as well as the newly-proposed Arabic cultural \& value alignment benchmark. Notably, AceGPT outperforms ChatGPT in the popular Vicuna-80 benchmark when evaluated with GPT-4, despite the benchmark's limited scale. % Natural Language Understanding (NLU) benchmark (i.e., ALUE) Codes, data, and models are in https://github.com/FreedomIntelligence/AceGPT.

DualFL: A Duality-based Federated Learning Algorithm with Communication Acceleration in the General Convex Regime

We propose a novel training algorithm called DualFL (Dualized Federated Learning), for solving a distributed optimization problem in federated learning. Our approach is based on a specific dual formulation of the federated learning problem. DualFL achieves communication acceleration under various settings on smoothness and strong convexity of the problem. Moreover, it theoretically guarantees the use of inexact local solvers, preserving its optimal communication complexity even with inexact local solutions. DualFL is the first federated learning algorithm that achieves communication acceleration, even when the cost function is either nonsmooth or non-strongly convex. Numerical results demonstrate that the practical performance of DualFL is comparable to those of state-of-the-art federated learning algorithms, and it is robust with respect to hyperparameter tuning.

FV-MgNet: Fully Connected V-cycle MgNet for Interpretable Time Series Forecasting

By investigating iterative methods for a constrained linear model, we propose a new class of fully connected V-cycle MgNet for long-term time series forecasting, which is one of the most difficult tasks in forecasting. MgNet is a CNN model that was proposed for image classification based on the multigrid (MG) methods for solving discretized partial differential equations (PDEs). We replace the convolutional operations with fully connected operations in the existing MgNet and then apply them to forecasting problems. Motivated by the V-cycle structure in MG, we further propose the FV-MgNet, a V-cycle version of the fully connected MgNet, to extract features hierarchically. By evaluating the performance of FV-MgNet on popular data sets and comparing it with state-of-the-art models, we show that the FV-MgNet achieves better results with less memory usage and faster inference speed. In addition, we develop ablation experiments to demonstrate that the structure of FV-MgNet is the best choice among the many variants.