MgNO: Efficient Parameterization of Linear Operators via Multigrid
Paper and Code
Oct 16, 2023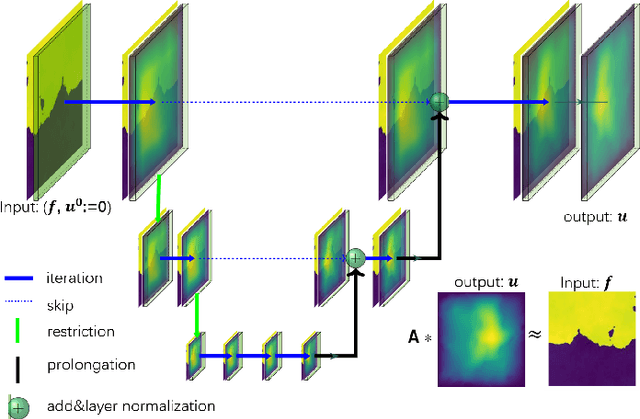
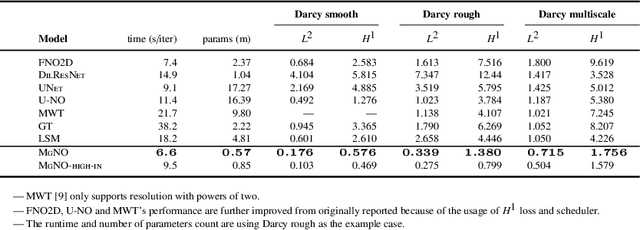
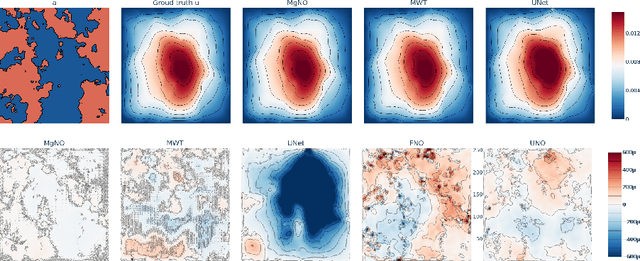
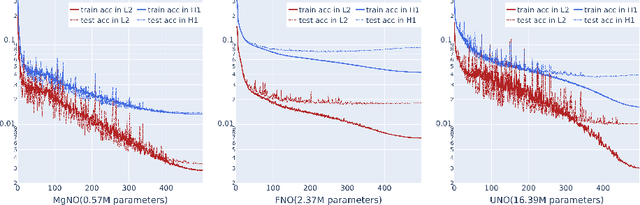
In this work, we propose a concise neural operator architecture for operator learning. Drawing an analogy with a conventional fully connected neural network, we define the neural operator as follows: the output of the $i$-th neuron in a nonlinear operator layer is defined by $\mathcal O_i(u) = \sigma\left( \sum_j \mathcal W_{ij} u + \mathcal B_{ij}\right)$. Here, $\mathcal W_{ij}$ denotes the bounded linear operator connecting $j$-th input neuron to $i$-th output neuron, and the bias $\mathcal B_{ij}$ takes the form of a function rather than a scalar. Given its new universal approximation property, the efficient parameterization of the bounded linear operators between two neurons (Banach spaces) plays a critical role. As a result, we introduce MgNO, utilizing multigrid structures to parameterize these linear operators between neurons. This approach offers both mathematical rigor and practical expressivity. Additionally, MgNO obviates the need for conventional lifting and projecting operators typically required in previous neural operators. Moreover, it seamlessly accommodates diverse boundary conditions. Our empirical observations reveal that MgNO exhibits superior ease of training compared to other CNN-based models, while also displaying a reduced susceptibility to overfitting when contrasted with spectral-type neural operators. We demonstrate the efficiency and accuracy of our method with consistently state-of-the-art performance on different types of partial differential equations (PDEs).
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge