Newton Informed Neural Operator for Computing Multiple Solutions of Nonlinear Partials Differential Equations

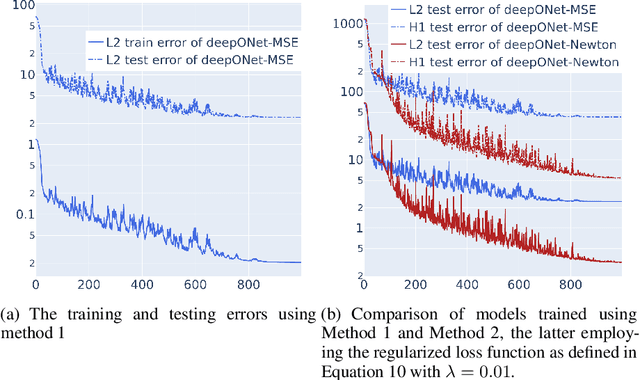
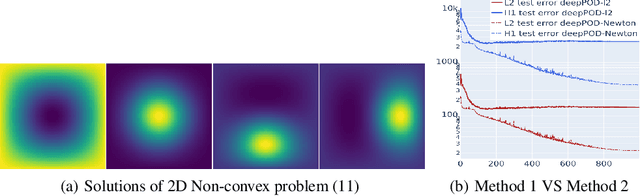
Solving nonlinear partial differential equations (PDEs) with multiple solutions using neural networks has found widespread applications in various fields such as physics, biology, and engineering. However, classical neural network methods for solving nonlinear PDEs, such as Physics-Informed Neural Networks (PINN), Deep Ritz methods, and DeepONet, often encounter challenges when confronted with the presence of multiple solutions inherent in the nonlinear problem. These methods may encounter ill-posedness issues. In this paper, we propose a novel approach called the Newton Informed Neural Operator, which builds upon existing neural network techniques to tackle nonlinearities. Our method combines classical Newton methods, addressing well-posed problems, and efficiently learns multiple solutions in a single learning process while requiring fewer supervised data points compared to existing neural network methods.

MgNO: Efficient Parameterization of Linear Operators via Multigrid

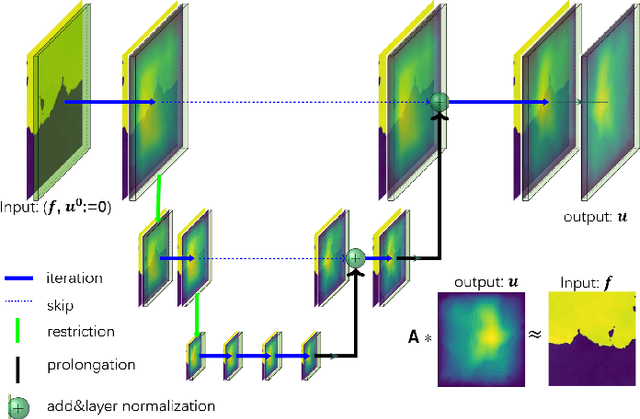
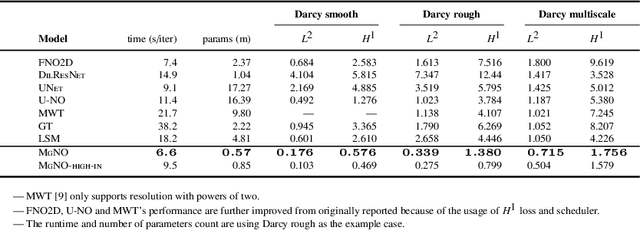
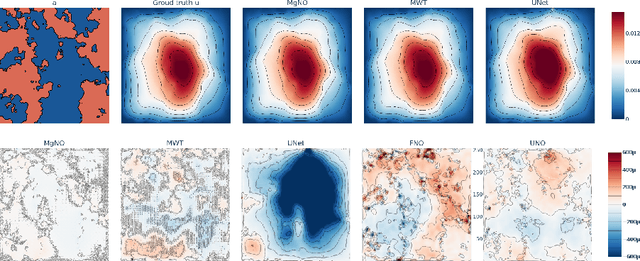
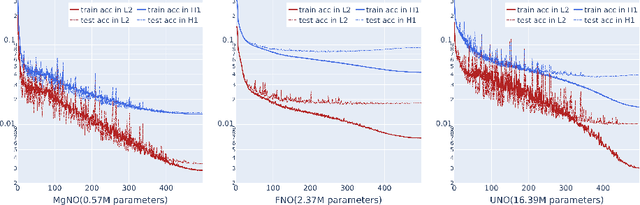
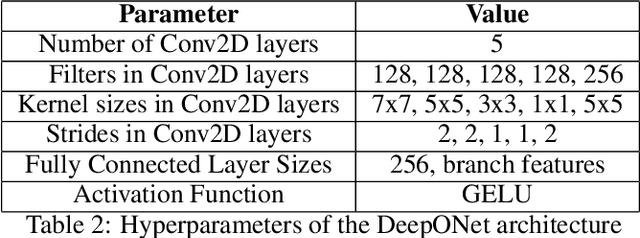
In this work, we propose a concise neural operator architecture for operator learning. Drawing an analogy with a conventional fully connected neural network, we define the neural operator as follows: the output of the $i$-th neuron in a nonlinear operator layer is defined by $\mathcal O_i(u) = \sigma\left( \sum_j \mathcal W_{ij} u + \mathcal B_{ij}\right)$. Here, $\mathcal W_{ij}$ denotes the bounded linear operator connecting $j$-th input neuron to $i$-th output neuron, and the bias $\mathcal B_{ij}$ takes the form of a function rather than a scalar. Given its new universal approximation property, the efficient parameterization of the bounded linear operators between two neurons (Banach spaces) plays a critical role. As a result, we introduce MgNO, utilizing multigrid structures to parameterize these linear operators between neurons. This approach offers both mathematical rigor and practical expressivity. Additionally, MgNO obviates the need for conventional lifting and projecting operators typically required in previous neural operators. Moreover, it seamlessly accommodates diverse boundary conditions. Our empirical observations reveal that MgNO exhibits superior ease of training compared to other CNN-based models, while also displaying a reduced susceptibility to overfitting when contrasted with spectral-type neural operators. We demonstrate the efficiency and accuracy of our method with consistently state-of-the-art performance on different types of partial differential equations (PDEs).

Framelet Message Passing

Graph neural networks (GNNs) have achieved champion in wide applications. Neural message passing is a typical key module for feature propagation by aggregating neighboring features. In this work, we propose a new message passing based on multiscale framelet transforms, called Framelet Message Passing. Different from traditional spatial methods, it integrates framelet representation of neighbor nodes from multiple hops away in node message update. We also propose a continuous message passing using neural ODE solvers. It turns both discrete and continuous cases can provably achieve network stability and limit oversmoothing due to the multiscale property of framelets. Numerical experiments on real graph datasets show that the continuous version of the framelet message passing significantly outperforms existing methods when learning heterogeneous graphs and achieves state-of-the-art performance on classic node classification tasks with low computational costs.

HT-Net: Hierarchical Transformer based Operator Learning Model for Multiscale PDEs

Complex nonlinear interplays of multiple scales give rise to many interesting physical phenomena and pose major difficulties for the computer simulation of multiscale PDE models in areas such as reservoir simulation, high frequency scattering and turbulence modeling. In this paper, we introduce a hierarchical transformer (HT) scheme to efficiently learn the solution operator for multiscale PDEs. We construct a hierarchical architecture with scale adaptive interaction range, such that the features can be computed in a nested manner and with a controllable linear cost. Self-attentions over a hierarchy of levels can be used to encode and decode the multiscale solution space over all scale ranges. In addition, we adopt an empirical $H^1$ loss function to counteract the spectral bias of the neural network approximation for multiscale functions. In the numerical experiments, we demonstrate the superior performance of the HT scheme compared with state-of-the-art (SOTA) methods for representative multiscale problems.

ACMP: Allen-Cahn Message Passing for Graph Neural Networks with Particle Phase Transition

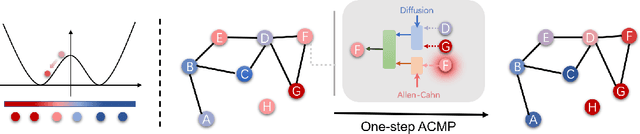
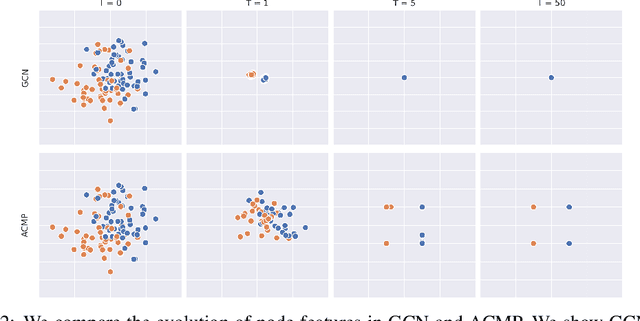
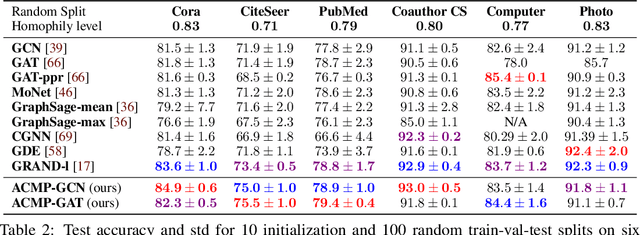
Neural message passing is a basic feature extraction unit for graph-structured data that takes account of the impact of neighboring node features in network propagation from one layer to the next. We model such process by an interacting particle system with attractive and repulsive forces and the Allen-Cahn force arising in the modeling of phase transition. The system is a reaction-diffusion process which can separate particles to different clusters. This induces an Allen-Cahn message passing (ACMP) for graph neural networks where the numerical iteration for the solution constitutes the message passing propagation. The mechanism behind ACMP is phase transition of particles which enables the formation of multi-clusters and thus GNNs prediction for node classification. ACMP can propel the network depth to hundreds of layers with theoretically proven strictly positive lower bound of the Dirichlet energy. It thus provides a deep model of GNNs which circumvents the common GNN problem of oversmoothing. Experiments for various real node classification datasets, with possible high homophily difficulty, show the GNNs with ACMP can achieve state of the art performance with no decay of Dirichlet energy.

Spectral Transform Forms Scalable Transformer

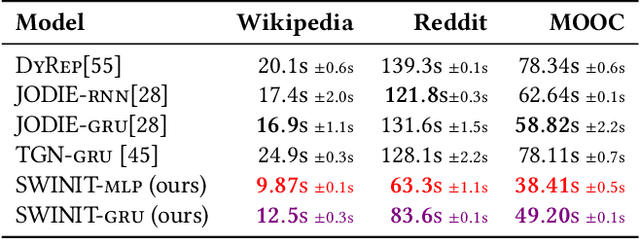
Many real-world relational systems, such as social networks and biological systems, contain dynamic interactions. When learning dynamic graph representation, it is essential to employ sequential temporal information and geometric structure. Mainstream work achieves topological embedding via message passing networks (e.g., GCN, GAT). The temporal evolution, on the other hand, is conventionally expressed via memory units (e.g., LSTM or GRU) that possess convenient information filtration in a gate mechanism. Though, such a design prevents large-scale input sequence due to the over-complicated encoding. This work learns from the philosophy of self-attention and proposes an efficient spectral-based neural unit that employs informative long-range temporal interaction. The developed spectral window unit (SWINIT) model predicts scalable dynamic graphs with assured efficiency. The architecture is assembled with a few simple effective computational blocks that constitute randomized SVD, MLP, and graph Framelet convolution. The SVD plus MLP module encodes the long-short-term feature evolution of the dynamic graph events. A fast framelet graph transform in the framelet convolution embeds the structural dynamics. Both strategies enhance the model's ability on scalable analysis. In particular, the iterative SVD approximation shrinks the computational complexity of attention to O(Nd\log(d)) for the dynamic graph with N edges and d edge features, and the multiscale transform of framelet convolution allows sufficient scalability in the network training. Our SWINIT achieves state-of-the-art performance on a variety of online continuous-time dynamic graph learning tasks, while compared to baseline methods, the number of its learnable parameters reduces by up to seven times.