Spectral Transform Forms Scalable Transformer
Paper and Code
Nov 15, 2021


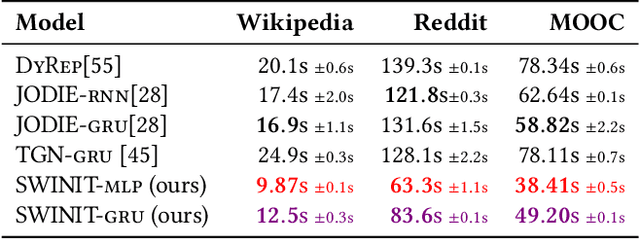
Many real-world relational systems, such as social networks and biological systems, contain dynamic interactions. When learning dynamic graph representation, it is essential to employ sequential temporal information and geometric structure. Mainstream work achieves topological embedding via message passing networks (e.g., GCN, GAT). The temporal evolution, on the other hand, is conventionally expressed via memory units (e.g., LSTM or GRU) that possess convenient information filtration in a gate mechanism. Though, such a design prevents large-scale input sequence due to the over-complicated encoding. This work learns from the philosophy of self-attention and proposes an efficient spectral-based neural unit that employs informative long-range temporal interaction. The developed spectral window unit (SWINIT) model predicts scalable dynamic graphs with assured efficiency. The architecture is assembled with a few simple effective computational blocks that constitute randomized SVD, MLP, and graph Framelet convolution. The SVD plus MLP module encodes the long-short-term feature evolution of the dynamic graph events. A fast framelet graph transform in the framelet convolution embeds the structural dynamics. Both strategies enhance the model's ability on scalable analysis. In particular, the iterative SVD approximation shrinks the computational complexity of attention to O(Nd\log(d)) for the dynamic graph with N edges and d edge features, and the multiscale transform of framelet convolution allows sufficient scalability in the network training. Our SWINIT achieves state-of-the-art performance on a variety of online continuous-time dynamic graph learning tasks, while compared to baseline methods, the number of its learnable parameters reduces by up to seven times.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge