ACMP: Allen-Cahn Message Passing for Graph Neural Networks with Particle Phase Transition

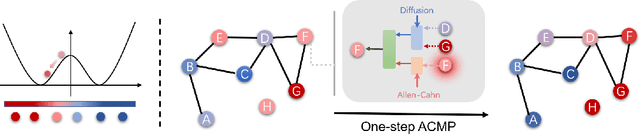
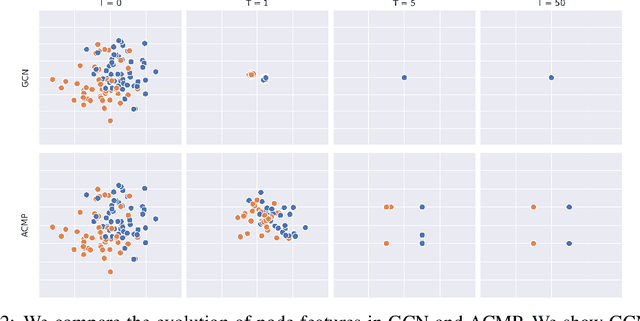
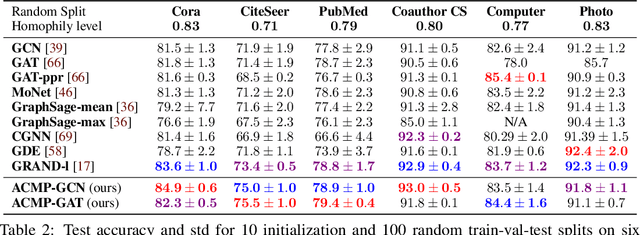
Neural message passing is a basic feature extraction unit for graph-structured data that takes account of the impact of neighboring node features in network propagation from one layer to the next. We model such process by an interacting particle system with attractive and repulsive forces and the Allen-Cahn force arising in the modeling of phase transition. The system is a reaction-diffusion process which can separate particles to different clusters. This induces an Allen-Cahn message passing (ACMP) for graph neural networks where the numerical iteration for the solution constitutes the message passing propagation. The mechanism behind ACMP is phase transition of particles which enables the formation of multi-clusters and thus GNNs prediction for node classification. ACMP can propel the network depth to hundreds of layers with theoretically proven strictly positive lower bound of the Dirichlet energy. It thus provides a deep model of GNNs which circumvents the common GNN problem of oversmoothing. Experiments for various real node classification datasets, with possible high homophily difficulty, show the GNNs with ACMP can achieve state of the art performance with no decay of Dirichlet energy.