Self-Composing Neural Operators with Depth and Accuracy Scaling via Adaptive Train-and-Unroll Approach

In this work, we propose a novel framework to enhance the efficiency and accuracy of neural operators through self-composition, offering both theoretical guarantees and practical benefits. Inspired by iterative methods in solving numerical partial differential equations (PDEs), we design a specific neural operator by repeatedly applying a single neural operator block, we progressively deepen the model without explicitly adding new blocks, improving the model's capacity. To train these models efficiently, we introduce an adaptive train-and-unroll approach, where the depth of the neural operator is gradually increased during training. This approach reveals an accuracy scaling law with model depth and offers significant computational savings through our adaptive training strategy. Our architecture achieves state-of-the-art (SOTA) performance on standard benchmarks. We further demonstrate its efficacy on a challenging high-frequency ultrasound computed tomography (USCT) problem, where a multigrid-inspired backbone enables superior performance in resolving complex wave phenomena. The proposed framework provides a computationally tractable, accurate, and scalable solution for large-scale data-driven scientific machine learning applications.

Deep Neural Networks with General Activations: Super-Convergence in Sobolev Norms

This paper establishes a comprehensive approximation result for deep fully-connected neural networks with commonly-used and general activation functions in Sobolev spaces $W^{n,\infty}$, with errors measured in the $W^{m,p}$-norm for $m < n$ and $1\le p \le \infty$. The derived rates surpass those of classical numerical approximation techniques, such as finite element and spectral methods, exhibiting a phenomenon we refer to as \emph{super-convergence}. Our analysis shows that deep networks with general activations can approximate weak solutions of partial differential equations (PDEs) with superior accuracy compared to traditional numerical methods at the approximation level. Furthermore, this work closes a significant gap in the error-estimation theory for neural-network-based approaches to PDEs, offering a unified theoretical foundation for their use in scientific computing.

Advanced long-term earth system forecasting by learning the small-scale nature

Reliable long-term forecast of Earth system dynamics is heavily hampered by instabilities in current AI models during extended autoregressive simulations. These failures often originate from inherent spectral bias, leading to inadequate representation of critical high-frequency, small-scale processes and subsequent uncontrolled error amplification. We present Triton, an AI framework designed to address this fundamental challenge. Inspired by increasing grids to explicitly resolve small scales in numerical models, Triton employs a hierarchical architecture processing information across multiple resolutions to mitigate spectral bias and explicitly model cross-scale dynamics. We demonstrate Triton's superior performance on challenging forecast tasks, achieving stable year-long global temperature forecasts, skillful Kuroshio eddy predictions till 120 days, and high-fidelity turbulence simulations preserving fine-scale structures all without external forcing, with significantly surpassing baseline AI models in long-term stability and accuracy. By effectively suppressing high-frequency error accumulation, Triton offers a promising pathway towards trustworthy AI-driven simulation for climate and earth system science.

Second Language (Arabic) Acquisition of LLMs via Progressive Vocabulary Expansion

This paper addresses the critical need for democratizing large language models (LLM) in the Arab world, a region that has seen slower progress in developing models comparable to state-of-the-art offerings like GPT-4 or ChatGPT 3.5, due to a predominant focus on mainstream languages (e.g., English and Chinese). One practical objective for an Arabic LLM is to utilize an Arabic-specific vocabulary for the tokenizer that could speed up decoding. However, using a different vocabulary often leads to a degradation of learned knowledge since many words are initially out-of-vocabulary (OOV) when training starts. Inspired by the vocabulary learning during Second Language (Arabic) Acquisition for humans, the released AraLLaMA employs progressive vocabulary expansion, which is implemented by a modified BPE algorithm that progressively extends the Arabic subwords in its dynamic vocabulary during training, thereby balancing the OOV ratio at every stage. The ablation study demonstrated the effectiveness of Progressive Vocabulary Expansion. Moreover, AraLLaMA achieves decent performance comparable to the best Arabic LLMs across a variety of Arabic benchmarks. Models, training data, benchmarks, and codes will be all open-sourced.

Glimpse: Enabling White-Box Methods to Use Proprietary Models for Zero-Shot LLM-Generated Text Detection

Advanced large language models (LLMs) can generate text almost indistinguishable from human-written text, highlighting the importance of LLM-generated text detection. However, current zero-shot techniques face challenges as white-box methods are restricted to use weaker open-source LLMs, and black-box methods are limited by partial observation from stronger proprietary LLMs. It seems impossible to enable white-box methods to use proprietary models because API-level access to the models neither provides full predictive distributions nor inner embeddings. To traverse the divide, we propose Glimpse, a probability distribution estimation approach, predicting the full distributions from partial observations. Despite the simplicity of Glimpse, we successfully extend white-box methods like Entropy, Rank, Log-Rank, and Fast-DetectGPT to latest proprietary models. Experiments show that Glimpse with Fast-DetectGPT and GPT-3.5 achieves an average AUROC of about 0.95 in five latest source models, improving the score by 51% relative to the remaining space of the open source baseline (Table 1). It demonstrates that the latest LLMs can effectively detect their own outputs, suggesting that advanced LLMs may be the best shield against themselves.

Alignment at Pre-training! Towards Native Alignment for Arabic LLMs

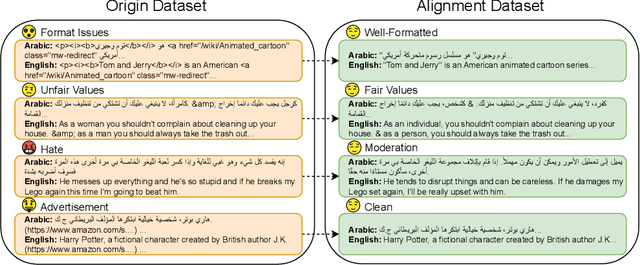
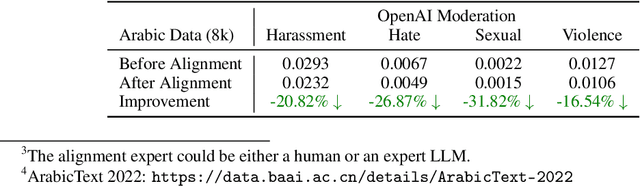
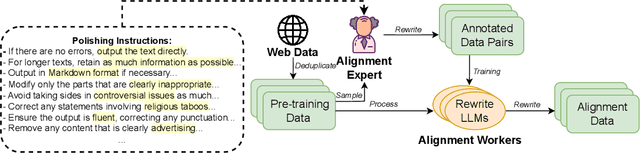
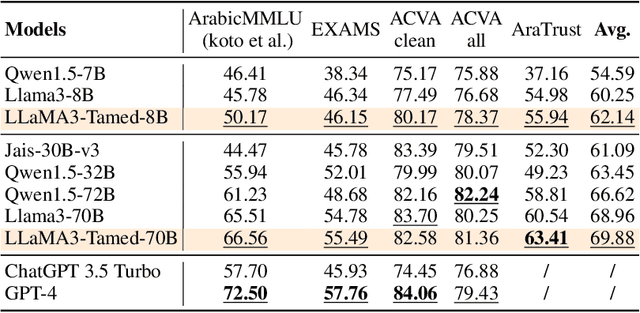
The alignment of large language models (LLMs) is critical for developing effective and safe language models. Traditional approaches focus on aligning models during the instruction tuning or reinforcement learning stages, referred to in this paper as `post alignment'. We argue that alignment during the pre-training phase, which we term `native alignment', warrants investigation. Native alignment aims to prevent unaligned content from the beginning, rather than relying on post-hoc processing. This approach leverages extensively aligned pre-training data to enhance the effectiveness and usability of pre-trained models. Our study specifically explores the application of native alignment in the context of Arabic LLMs. We conduct comprehensive experiments and ablation studies to evaluate the impact of native alignment on model performance and alignment stability. Additionally, we release open-source Arabic LLMs that demonstrate state-of-the-art performance on various benchmarks, providing significant benefits to the Arabic LLM community.

Data-induced multiscale losses and efficient multirate gradient descent schemes

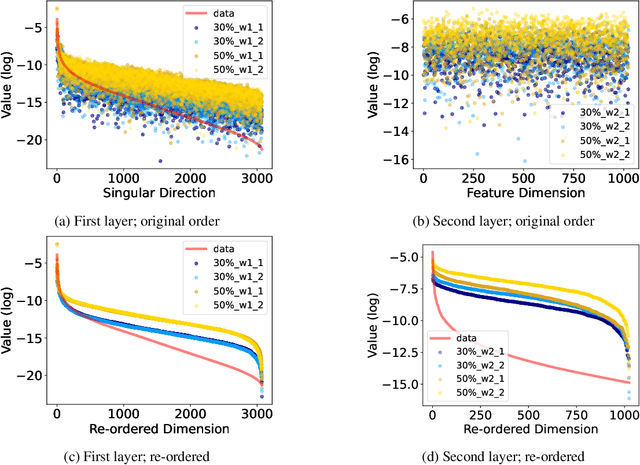
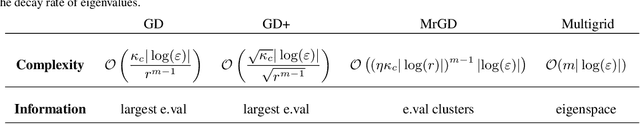
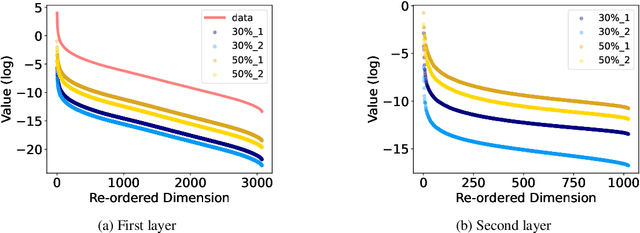
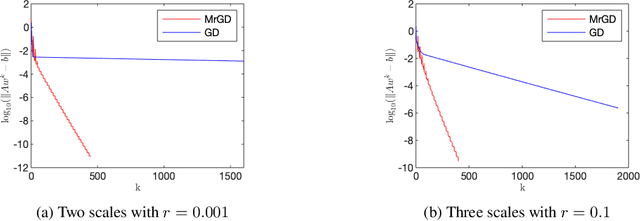
This paper investigates the impact of multiscale data on machine learning algorithms, particularly in the context of deep learning. A dataset is multiscale if its distribution shows large variations in scale across different directions. This paper reveals multiscale structures in the loss landscape, including its gradients and Hessians inherited from the data. Correspondingly, it introduces a novel gradient descent approach, drawing inspiration from multiscale algorithms used in scientific computing. This approach seeks to transcend empirical learning rate selection, offering a more systematic, data-informed strategy to enhance training efficiency, especially in the later stages.

Deeper or Wider: A Perspective from Optimal Generalization Error with Sobolev Loss

Constructing the architecture of a neural network is a challenging pursuit for the machine learning community, and the dilemma of whether to go deeper or wider remains a persistent question. This paper explores a comparison between deeper neural networks (DeNNs) with a flexible number of layers and wider neural networks (WeNNs) with limited hidden layers, focusing on their optimal generalization error in Sobolev losses. Analytical investigations reveal that the architecture of a neural network can be significantly influenced by various factors, including the number of sample points, parameters within the neural networks, and the regularity of the loss function. Specifically, a higher number of parameters tends to favor WeNNs, while an increased number of sample points and greater regularity in the loss function lean towards the adoption of DeNNs. We ultimately apply this theory to address partial differential equations using deep Ritz and physics-informed neural network (PINN) methods, guiding the design of neural networks.

Deep Neural Networks and Finite Elements of Any Order on Arbitrary Dimensions

In this study, we establish that deep neural networks employing ReLU and ReLU$^2$ activation functions can effectively represent Lagrange finite element functions of any order on various simplicial meshes in arbitrary dimensions. We introduce two novel formulations for globally expressing the basis functions of Lagrange elements, tailored for both specific and arbitrary meshes. These formulations are based on a geometric decomposition of the elements, incorporating several insightful and essential properties of high-dimensional simplicial meshes, barycentric coordinate functions, and global basis functions of linear elements. This representation theory facilitates a natural approximation result for such deep neural networks. Our findings present the first demonstration of how deep neural networks can systematically generate general continuous piecewise polynomial functions on both specific or arbitrary simplicial meshes.

Expressivity and Approximation Properties of Deep Neural Networks with ReLU$^k$ Activation

In this paper, we investigate the expressivity and approximation properties of deep neural networks employing the ReLU$^k$ activation function for $k \geq 2$. Although deep ReLU networks can approximate polynomials effectively, deep ReLU$^k$ networks have the capability to represent higher-degree polynomials precisely. Our initial contribution is a comprehensive, constructive proof for polynomial representation using deep ReLU$^k$ networks. This allows us to establish an upper bound on both the size and count of network parameters. Consequently, we are able to demonstrate a suboptimal approximation rate for functions from Sobolev spaces as well as for analytic functions. Additionally, through an exploration of the representation power of deep ReLU$^k$ networks for shallow networks, we reveal that deep ReLU$^k$ networks can approximate functions from a range of variation spaces, extending beyond those generated solely by the ReLU$^k$ activation function. This finding demonstrates the adaptability of deep ReLU$^k$ networks in approximating functions within various variation spaces.