Yahong Yang
On the Dimension-Free Approximation of Deep Neural Networks for Symmetric Korobov Functions
Nov 16, 2025


Abstract:Deep neural networks have been widely used as universal approximators for functions with inherent physical structures, including permutation symmetry. In this paper, we construct symmetric deep neural networks to approximate symmetric Korobov functions and prove that both the convergence rate and the constant prefactor scale at most polynomially with respect to the ambient dimension. This represents a substantial improvement over prior approximation guarantees that suffer from the curse of dimensionality. Building on these approximation bounds, we further derive a generalization-error rate for learning symmetric Korobov functions whose leading factors likewise avoid the curse of dimensionality.
Deep Neural Networks with General Activations: Super-Convergence in Sobolev Norms
Aug 07, 2025Abstract:This paper establishes a comprehensive approximation result for deep fully-connected neural networks with commonly-used and general activation functions in Sobolev spaces $W^{n,\infty}$, with errors measured in the $W^{m,p}$-norm for $m < n$ and $1\le p \le \infty$. The derived rates surpass those of classical numerical approximation techniques, such as finite element and spectral methods, exhibiting a phenomenon we refer to as \emph{super-convergence}. Our analysis shows that deep networks with general activations can approximate weak solutions of partial differential equations (PDEs) with superior accuracy compared to traditional numerical methods at the approximation level. Furthermore, this work closes a significant gap in the error-estimation theory for neural-network-based approaches to PDEs, offering a unified theoretical foundation for their use in scientific computing.
An Imbalanced Learning-based Sampling Method for Physics-informed Neural Networks
Jan 20, 2025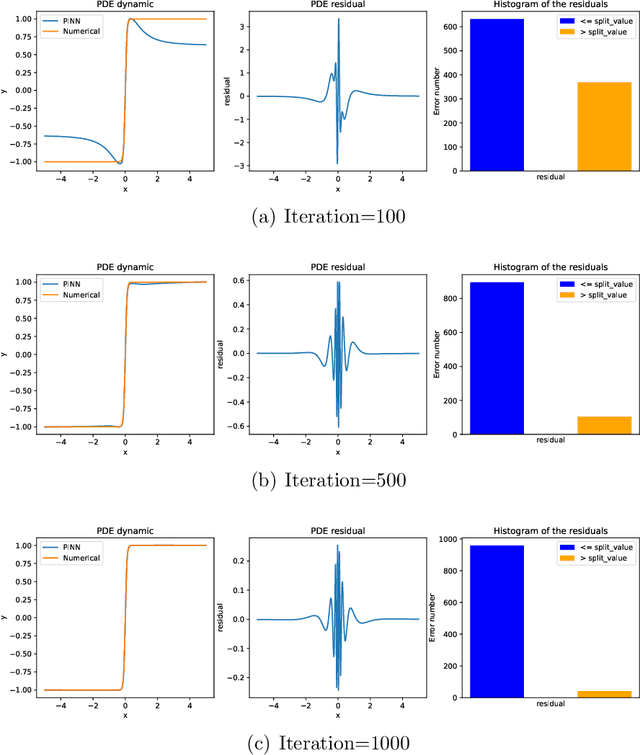
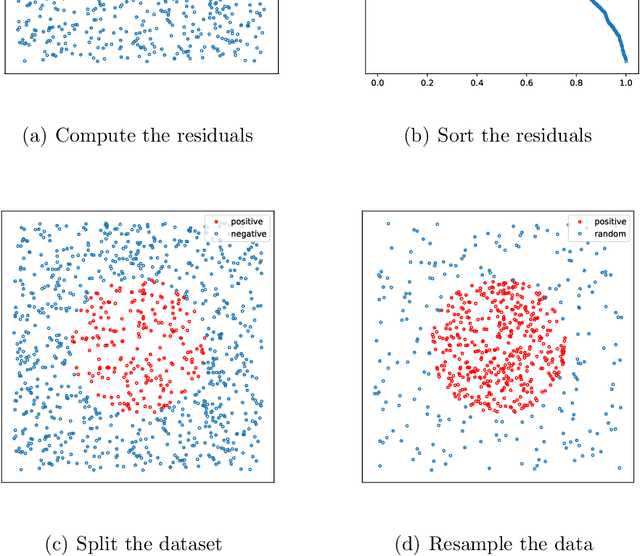

Abstract:This paper introduces Residual-based Smote (RSmote), an innovative local adaptive sampling technique tailored to improve the performance of Physics-Informed Neural Networks (PINNs) through imbalanced learning strategies. Traditional residual-based adaptive sampling methods, while effective in enhancing PINN accuracy, often struggle with efficiency and high memory consumption, particularly in high-dimensional problems. RSmote addresses these challenges by targeting regions with high residuals and employing oversampling techniques from imbalanced learning to refine the sampling process. Our approach is underpinned by a rigorous theoretical analysis that supports the effectiveness of RSmote in managing computational resources more efficiently. Through extensive evaluations, we benchmark RSmote against the state-of-the-art Residual-based Adaptive Distribution (RAD) method across a variety of dimensions and differential equations. The results demonstrate that RSmote not only achieves or exceeds the accuracy of RAD but also significantly reduces memory usage, making it particularly advantageous in high-dimensional scenarios. These contributions position RSmote as a robust and resource-efficient solution for solving complex partial differential equations, especially when computational constraints are a critical consideration.
Quantifying Training Difficulty and Accelerating Convergence in Neural Network-Based PDE Solvers
Oct 08, 2024
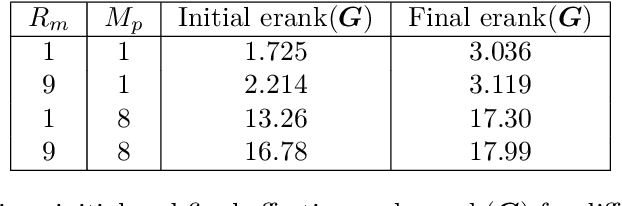

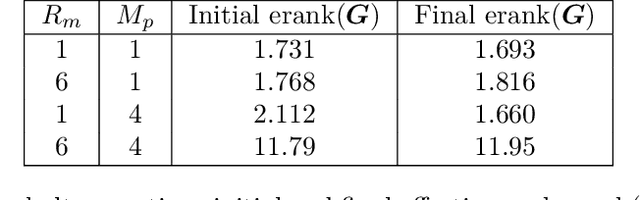
Abstract:Neural network-based methods have emerged as powerful tools for solving partial differential equations (PDEs) in scientific and engineering applications, particularly when handling complex domains or incorporating empirical data. These methods leverage neural networks as basis functions to approximate PDE solutions. However, training such networks can be challenging, often resulting in limited accuracy. In this paper, we investigate the training dynamics of neural network-based PDE solvers with a focus on the impact of initialization techniques. We assess training difficulty by analyzing the eigenvalue distribution of the kernel and apply the concept of effective rank to quantify this difficulty, where a larger effective rank correlates with faster convergence of the training error. Building upon this, we discover through theoretical analysis and numerical experiments that two initialization techniques, partition of unity (PoU) and variance scaling (VS), enhance the effective rank, thereby accelerating the convergence of training error. Furthermore, comprehensive experiments using popular PDE-solving frameworks, such as PINN, Deep Ritz, and the operator learning framework DeepOnet, confirm that these initialization techniques consistently speed up convergence, in line with our theoretical findings.
DeepONet for Solving PDEs: Generalization Analysis in Sobolev Training
Oct 06, 2024
Abstract:In this paper, we investigate the application of operator learning, specifically DeepONet, to solve partial differential equations (PDEs). Unlike function learning methods that require training separate neural networks for each PDE, operator learning generalizes across different PDEs without retraining. We focus on the performance of DeepONet in Sobolev training, addressing two key questions: the approximation ability of deep branch and trunk networks, and the generalization error in Sobolev norms. Our findings highlight that deep branch networks offer significant performance benefits, while trunk networks are best kept simple. Moreover, standard sampling methods without adding derivative information in the encoding part are sufficient for minimizing generalization error in Sobolev training, based on generalization analysis. This paper fills a theoretical gap by providing error estimations for a wide range of physics-informed machine learning models and applications.
Automatic Differentiation is Essential in Training Neural Networks for Solving Differential Equations
May 23, 2024



Abstract:Neural network-based approaches have recently shown significant promise in solving partial differential equations (PDEs) in science and engineering, especially in scenarios featuring complex domains or the incorporation of empirical data. One advantage of the neural network method for PDEs lies in its automatic differentiation (AD), which necessitates only the sample points themselves, unlike traditional finite difference (FD) approximations that require nearby local points to compute derivatives. In this paper, we quantitatively demonstrate the advantage of AD in training neural networks. The concept of truncated entropy is introduced to characterize the training property. Specifically, through comprehensive experimental and theoretical analyses conducted on random feature models and two-layer neural networks, we discover that the defined truncated entropy serves as a reliable metric for quantifying the residual loss of random feature models and the training speed of neural networks for both AD and FD methods. Our experimental and theoretical analyses demonstrate that, from a training perspective, AD outperforms FD in solving partial differential equations.
Newton Informed Neural Operator for Computing Multiple Solutions of Nonlinear Partials Differential Equations
May 23, 2024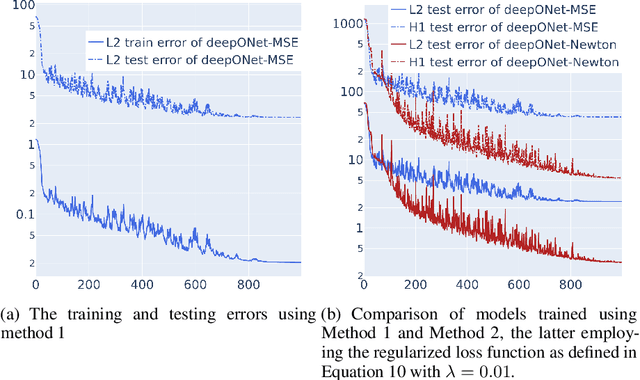

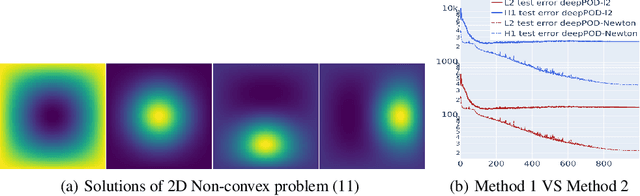
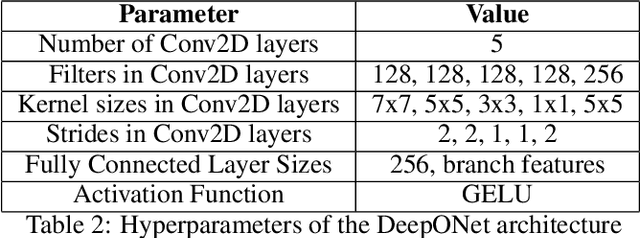
Abstract:Solving nonlinear partial differential equations (PDEs) with multiple solutions using neural networks has found widespread applications in various fields such as physics, biology, and engineering. However, classical neural network methods for solving nonlinear PDEs, such as Physics-Informed Neural Networks (PINN), Deep Ritz methods, and DeepONet, often encounter challenges when confronted with the presence of multiple solutions inherent in the nonlinear problem. These methods may encounter ill-posedness issues. In this paper, we propose a novel approach called the Newton Informed Neural Operator, which builds upon existing neural network techniques to tackle nonlinearities. Our method combines classical Newton methods, addressing well-posed problems, and efficiently learns multiple solutions in a single learning process while requiring fewer supervised data points compared to existing neural network methods.
Deeper or Wider: A Perspective from Optimal Generalization Error with Sobolev Loss
Jan 31, 2024

Abstract:Constructing the architecture of a neural network is a challenging pursuit for the machine learning community, and the dilemma of whether to go deeper or wider remains a persistent question. This paper explores a comparison between deeper neural networks (DeNNs) with a flexible number of layers and wider neural networks (WeNNs) with limited hidden layers, focusing on their optimal generalization error in Sobolev losses. Analytical investigations reveal that the architecture of a neural network can be significantly influenced by various factors, including the number of sample points, parameters within the neural networks, and the regularity of the loss function. Specifically, a higher number of parameters tends to favor WeNNs, while an increased number of sample points and greater regularity in the loss function lean towards the adoption of DeNNs. We ultimately apply this theory to address partial differential equations using deep Ritz and physics-informed neural network (PINN) methods, guiding the design of neural networks.
Optimal Deep Neural Network Approximation for Korobov Functions with respect to Sobolev Norms
Nov 08, 2023

Abstract:This paper establishes the nearly optimal rate of approximation for deep neural networks (DNNs) when applied to Korobov functions, effectively overcoming the curse of dimensionality. The approximation results presented in this paper are measured with respect to $L_p$ norms and $H^1$ norms. Our achieved approximation rate demonstrates a remarkable "super-convergence" rate, outperforming traditional methods and any continuous function approximator. These results are non-asymptotic, providing error bounds that consider both the width and depth of the networks simultaneously.
Homotopy Relaxation Training Algorithms for Infinite-Width Two-Layer ReLU Neural Networks
Sep 26, 2023Abstract:In this paper, we present a novel training approach called the Homotopy Relaxation Training Algorithm (HRTA), aimed at accelerating the training process in contrast to traditional methods. Our algorithm incorporates two key mechanisms: one involves building a homotopy activation function that seamlessly connects the linear activation function with the ReLU activation function; the other technique entails relaxing the homotopy parameter to enhance the training refinement process. We have conducted an in-depth analysis of this novel method within the context of the neural tangent kernel (NTK), revealing significantly improved convergence rates. Our experimental results, especially when considering networks with larger widths, validate the theoretical conclusions. This proposed HRTA exhibits the potential for other activation functions and deep neural networks.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge