Improving GBDT Performance on Imbalanced Datasets: An Empirical Study of Class-Balanced Loss Functions

Class imbalance remains a significant challenge in machine learning, particularly for tabular data classification tasks. While Gradient Boosting Decision Trees (GBDT) models have proven highly effective for such tasks, their performance can be compromised when dealing with imbalanced datasets. This paper presents the first comprehensive study on adapting class-balanced loss functions to three GBDT algorithms across various tabular classification tasks, including binary, multi-class, and multi-label classification. We conduct extensive experiments on multiple datasets to evaluate the impact of class-balanced losses on different GBDT models, establishing a valuable benchmark. Our results demonstrate the potential of class-balanced loss functions to enhance GBDT performance on imbalanced datasets, offering a robust approach for practitioners facing class imbalance challenges in real-world applications. Additionally, we introduce a Python package that facilitates the integration of class-balanced loss functions into GBDT workflows, making these advanced techniques accessible to a wider audience.

Robust-GBDT: A Novel Gradient Boosting Model for Noise-Robust Classification

Robust boosting algorithms have emerged as alternative solutions to traditional boosting techniques for addressing label noise in classification tasks. However, these methods have predominantly focused on binary classification, limiting their applicability to multi-class tasks. Furthermore, they encounter challenges with imbalanced datasets, missing values, and computational efficiency. In this paper, we establish that the loss function employed in advanced Gradient Boosting Decision Trees (GBDT), particularly Newton's method-based GBDT, need not necessarily exhibit global convexity. Instead, the loss function only requires convexity within a specific region. Consequently, these GBDT models can leverage the benefits of nonconvex robust loss functions, making them resilient to noise. Building upon this theoretical insight, we introduce a new noise-robust boosting model called Robust-GBDT, which seamlessly integrates the advanced GBDT framework with robust losses. Additionally, we enhance the existing robust loss functions and introduce a novel robust loss function, Robust Focal Loss, designed to address class imbalance. As a result, Robust-GBDT generates more accurate predictions, significantly enhancing its generalization capabilities, especially in scenarios marked by label noise and class imbalance. Furthermore, Robust-GBDT is user-friendly and can easily integrate existing open-source code, enabling it to effectively handle complex datasets while improving computational efficiency. Numerous experiments confirm the superiority of Robust-GBDT over other noise-robust methods.

NCART: Neural Classification and Regression Tree for Tabular Data

Deep learning models have become popular in the analysis of tabular data, as they address the limitations of decision trees and enable valuable applications like semi-supervised learning, online learning, and transfer learning. However, these deep-learning approaches often encounter a trade-off. On one hand, they can be computationally expensive when dealing with large-scale or high-dimensional datasets. On the other hand, they may lack interpretability and may not be suitable for small-scale datasets. In this study, we propose a novel interpretable neural network called Neural Classification and Regression Tree (NCART) to overcome these challenges. NCART is a modified version of Residual Networks that replaces fully-connected layers with multiple differentiable oblivious decision trees. By integrating decision trees into the architecture, NCART maintains its interpretability while benefiting from the end-to-end capabilities of neural networks. The simplicity of the NCART architecture makes it well-suited for datasets of varying sizes and reduces computational costs compared to state-of-the-art deep learning models. Extensive numerical experiments demonstrate the superior performance of NCART compared to existing deep learning models, establishing it as a strong competitor to tree-based models.

Generating Adversarial Examples with Better Transferability via Masking Unimportant Parameters of Surrogate Model

Deep neural networks (DNNs) have been shown to be vulnerable to adversarial examples. Moreover, the transferability of the adversarial examples has received broad attention in recent years, which means that adversarial examples crafted by a surrogate model can also attack unknown models. This phenomenon gave birth to the transfer-based adversarial attacks, which aim to improve the transferability of the generated adversarial examples. In this paper, we propose to improve the transferability of adversarial examples in the transfer-based attack via masking unimportant parameters (MUP). The key idea in MUP is to refine the pretrained surrogate models to boost the transfer-based attack. Based on this idea, a Taylor expansion-based metric is used to evaluate the parameter importance score and the unimportant parameters are masked during the generation of adversarial examples. This process is simple, yet can be naturally combined with various existing gradient-based optimizers for generating adversarial examples, thus further improving the transferability of the generated adversarial examples. Extensive experiments are conducted to validate the effectiveness of the proposed MUP-based methods.

TRBoost: A Generic Gradient Boosting Machine based on Trust-region Method

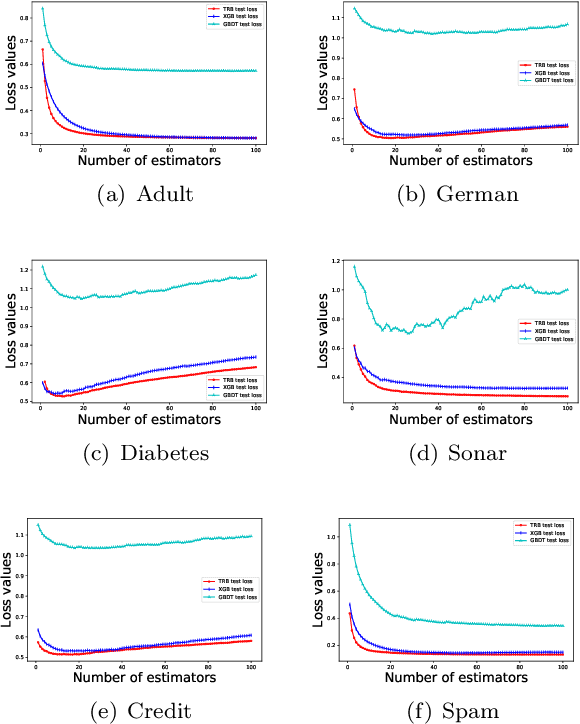
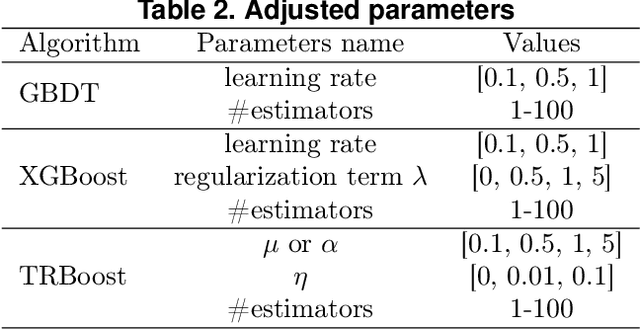
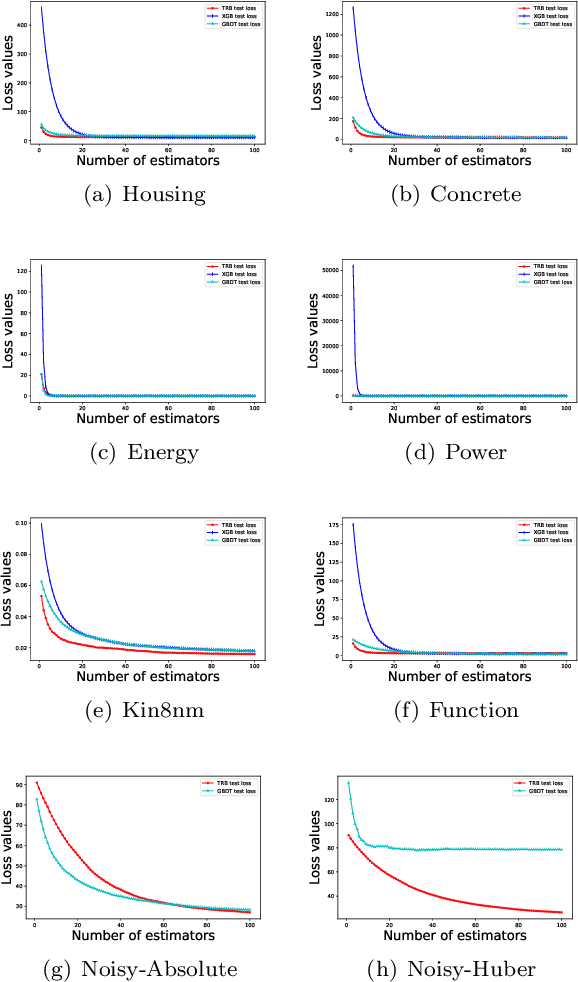
Gradient Boosting Machines (GBMs) are derived from Taylor expansion in functional space and have achieved state-of-the-art results on a variety of problems. However, there is a dilemma for GBMs to maintain a balance between performance and generality. Specifically, gradient descent-based GBMs employ the first-order Taylor expansion to make them appropriate for all loss functions. And Newton's method-based GBMs use the positive hessian information to achieve better performance at the expense of generality. In this paper, a generic Gradient Boosting Machine called Trust-region Boosting (TRBoost) is presented to maintain this balance. In each iteration, we apply a constrained quadratic model to approximate the objective and solve it by the Trust-region algorithm to obtain a new learner. TRBoost offers the benefit that we do not need the hessian to be positive definite, which generalizes GBMs to suit arbitrary loss functions while keeping up the good performance as the second-order algorithm. Several numerical experiments are conducted to confirm that TRBoost is not only as general as the first-order GBMs but also able to get competitive results with the second-order GBMs.