Junkai Man
TRBoost: A Generic Gradient Boosting Machine based on Trust-region Method
Oct 08, 2022
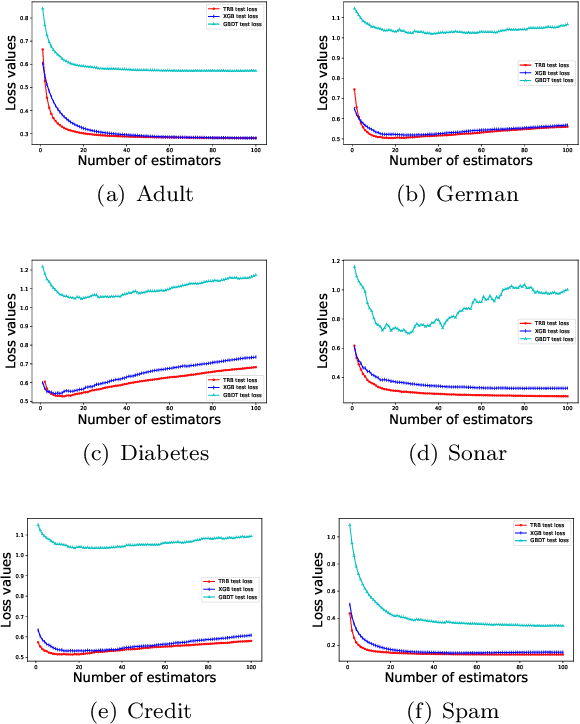
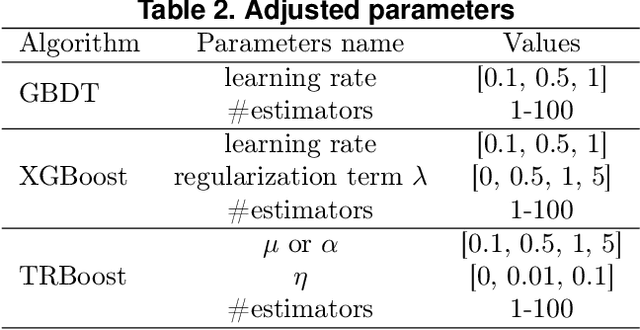
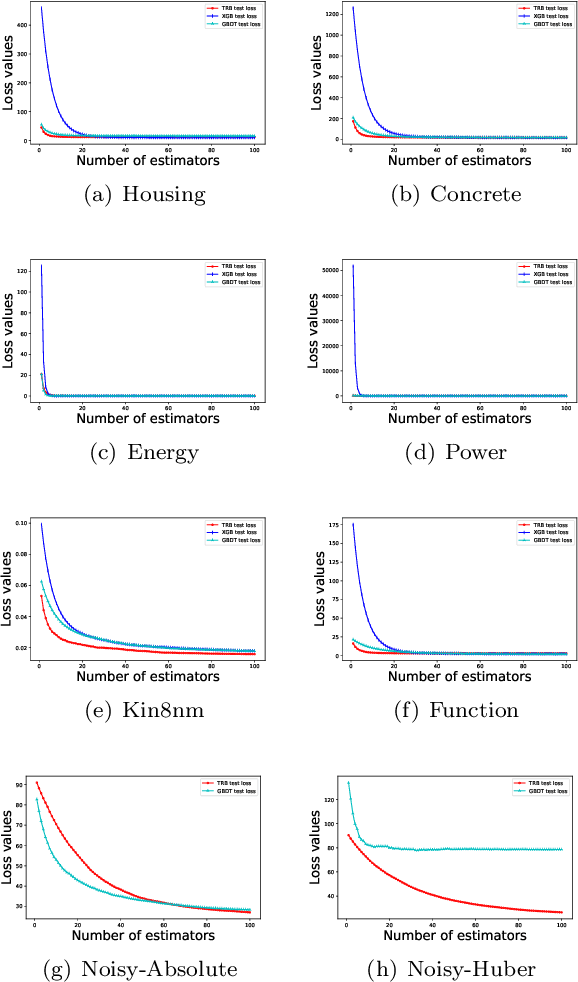
Abstract:Gradient Boosting Machines (GBMs) are derived from Taylor expansion in functional space and have achieved state-of-the-art results on a variety of problems. However, there is a dilemma for GBMs to maintain a balance between performance and generality. Specifically, gradient descent-based GBMs employ the first-order Taylor expansion to make them appropriate for all loss functions. And Newton's method-based GBMs use the positive hessian information to achieve better performance at the expense of generality. In this paper, a generic Gradient Boosting Machine called Trust-region Boosting (TRBoost) is presented to maintain this balance. In each iteration, we apply a constrained quadratic model to approximate the objective and solve it by the Trust-region algorithm to obtain a new learner. TRBoost offers the benefit that we do not need the hessian to be positive definite, which generalizes GBMs to suit arbitrary loss functions while keeping up the good performance as the second-order algorithm. Several numerical experiments are conducted to confirm that TRBoost is not only as general as the first-order GBMs but also able to get competitive results with the second-order GBMs.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge