Quantifying Training Difficulty and Accelerating Convergence in Neural Network-Based PDE Solvers
Paper and Code
Oct 08, 2024
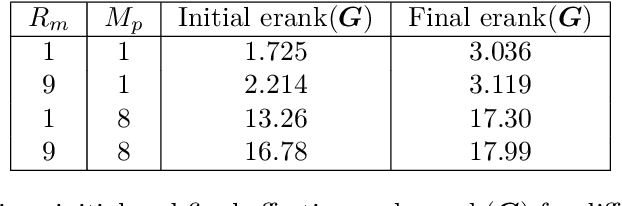

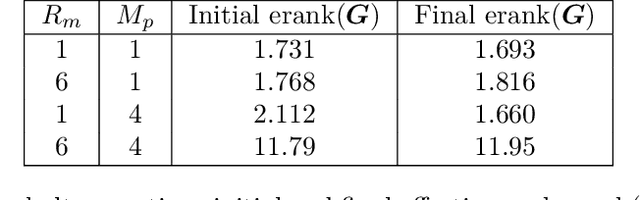
Neural network-based methods have emerged as powerful tools for solving partial differential equations (PDEs) in scientific and engineering applications, particularly when handling complex domains or incorporating empirical data. These methods leverage neural networks as basis functions to approximate PDE solutions. However, training such networks can be challenging, often resulting in limited accuracy. In this paper, we investigate the training dynamics of neural network-based PDE solvers with a focus on the impact of initialization techniques. We assess training difficulty by analyzing the eigenvalue distribution of the kernel and apply the concept of effective rank to quantify this difficulty, where a larger effective rank correlates with faster convergence of the training error. Building upon this, we discover through theoretical analysis and numerical experiments that two initialization techniques, partition of unity (PoU) and variance scaling (VS), enhance the effective rank, thereby accelerating the convergence of training error. Furthermore, comprehensive experiments using popular PDE-solving frameworks, such as PINN, Deep Ritz, and the operator learning framework DeepOnet, confirm that these initialization techniques consistently speed up convergence, in line with our theoretical findings.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge