Quantifying Training Difficulty and Accelerating Convergence in Neural Network-Based PDE Solvers

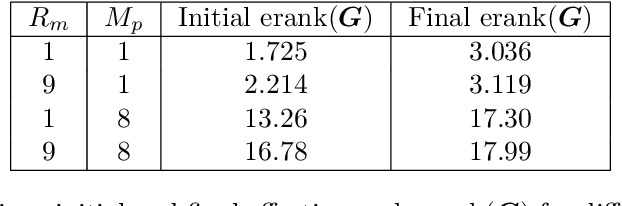
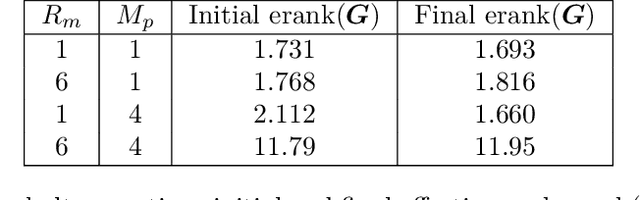
Neural network-based methods have emerged as powerful tools for solving partial differential equations (PDEs) in scientific and engineering applications, particularly when handling complex domains or incorporating empirical data. These methods leverage neural networks as basis functions to approximate PDE solutions. However, training such networks can be challenging, often resulting in limited accuracy. In this paper, we investigate the training dynamics of neural network-based PDE solvers with a focus on the impact of initialization techniques. We assess training difficulty by analyzing the eigenvalue distribution of the kernel and apply the concept of effective rank to quantify this difficulty, where a larger effective rank correlates with faster convergence of the training error. Building upon this, we discover through theoretical analysis and numerical experiments that two initialization techniques, partition of unity (PoU) and variance scaling (VS), enhance the effective rank, thereby accelerating the convergence of training error. Furthermore, comprehensive experiments using popular PDE-solving frameworks, such as PINN, Deep Ritz, and the operator learning framework DeepOnet, confirm that these initialization techniques consistently speed up convergence, in line with our theoretical findings.

Demystifying Lazy Training of Neural Networks from a Macroscopic Viewpoint

In this paper, we advance the understanding of neural network training dynamics by examining the intricate interplay of various factors introduced by weight parameters in the initialization process. Motivated by the foundational work of Luo et al. (J. Mach. Learn. Res., Vol. 22, Iss. 1, No. 71, pp 3327-3373), we explore the gradient descent dynamics of neural networks through the lens of macroscopic limits, where we analyze its behavior as width $m$ tends to infinity. Our study presents a unified approach with refined techniques designed for multi-layer fully connected neural networks, which can be readily extended to other neural network architectures. Our investigation reveals that gradient descent can rapidly drive deep neural networks to zero training loss, irrespective of the specific initialization schemes employed by weight parameters, provided that the initial scale of the output function $\kappa$ surpasses a certain threshold. This regime, characterized as the theta-lazy area, accentuates the predominant influence of the initial scale $\kappa$ over other factors on the training behavior of neural networks. Furthermore, our approach draws inspiration from the Neural Tangent Kernel (NTK) paradigm, and we expand its applicability. While NTK typically assumes that $\lim_{m\to\infty}\frac{\log \kappa}{\log m}=\frac{1}{2}$, and imposes each weight parameters to scale by the factor $\frac{1}{\sqrt{m}}$, in our theta-lazy regime, we discard the factor and relax the conditions to $\lim_{m\to\infty}\frac{\log \kappa}{\log m}>0$. Similar to NTK, the behavior of overparameterized neural networks within the theta-lazy regime trained by gradient descent can be effectively described by a specific kernel. Through rigorous analysis, our investigation illuminates the pivotal role of $\kappa$ in governing the training dynamics of neural networks.

A priori Estimates for Deep Residual Network in Continuous-time Reinforcement Learning

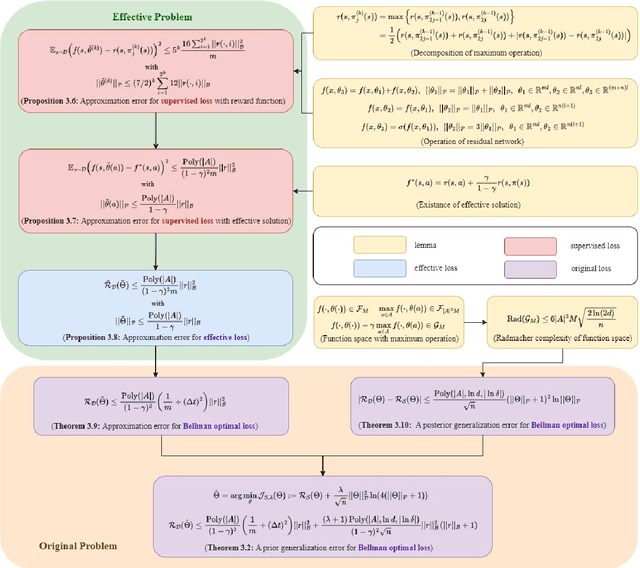
Deep reinforcement learning excels in numerous large-scale practical applications. However, existing performance analyses ignores the unique characteristics of continuous-time control problems, is unable to directly estimate the generalization error of the Bellman optimal loss and require a boundedness assumption. Our work focuses on continuous-time control problems and proposes a method that is applicable to all such problems where the transition function satisfies semi-group and Lipschitz properties. Under this method, we can directly analyze the \emph{a priori} generalization error of the Bellman optimal loss. The core of this method lies in two transformations of the loss function. To complete the transformation, we propose a decomposition method for the maximum operator. Additionally, this analysis method does not require a boundedness assumption. Finally, we obtain an \emph{a priori} generalization error without the curse of dimensionality.

Empirical Phase Diagram for Three-layer Neural Networks with Infinite Width

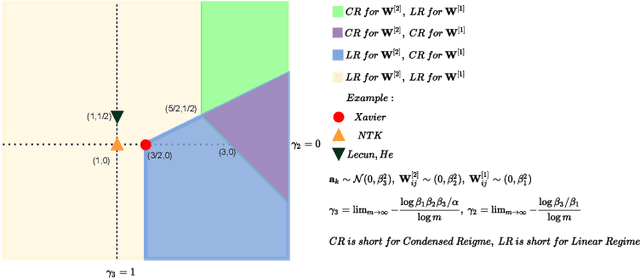
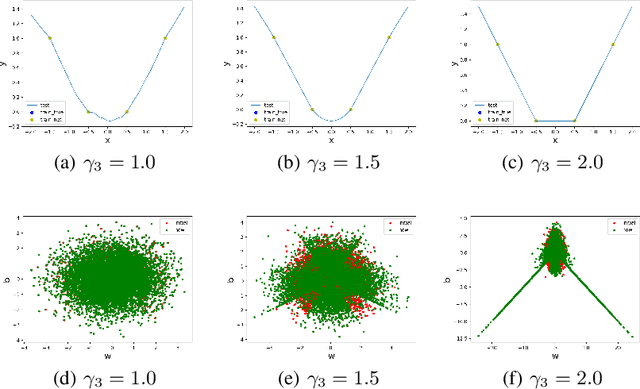
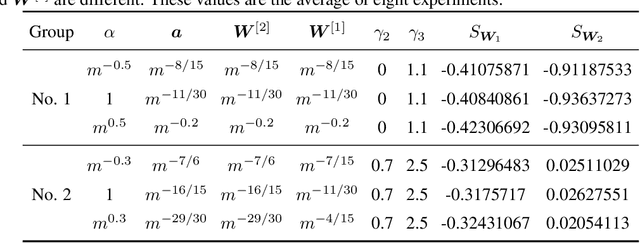
Substantial work indicates that the dynamics of neural networks (NNs) is closely related to their initialization of parameters. Inspired by the phase diagram for two-layer ReLU NNs with infinite width (Luo et al., 2021), we make a step towards drawing a phase diagram for three-layer ReLU NNs with infinite width. First, we derive a normalized gradient flow for three-layer ReLU NNs and obtain two key independent quantities to distinguish different dynamical regimes for common initialization methods. With carefully designed experiments and a large computation cost, for both synthetic datasets and real datasets, we find that the dynamics of each layer also could be divided into a linear regime and a condensed regime, separated by a critical regime. The criteria is the relative change of input weights (the input weight of a hidden neuron consists of the weight from its input layer to the hidden neuron and its bias term) as the width approaches infinity during the training, which tends to $0$, $+\infty$ and $O(1)$, respectively. In addition, we also demonstrate that different layers can lie in different dynamical regimes in a training process within a deep NN. In the condensed regime, we also observe the condensation of weights in isolated orientations with low complexity. Through experiments under three-layer condition, our phase diagram suggests a complicated dynamical regimes consisting of three possible regimes, together with their mixture, for deep NNs and provides a guidance for studying deep NNs in different initialization regimes, which reveals the possibility of completely different dynamics emerging within a deep NN for its different layers.