Analyzing and Bridging the Gap between Maximizing Total Reward and Discounted Reward in Deep Reinforcement Learning

In deep reinforcement learning applications, maximizing discounted reward is often employed instead of maximizing total reward to ensure the convergence and stability of algorithms, even though the performance metric for evaluating the policy remains the total reward. However, the optimal policies corresponding to these two objectives may not always be consistent. To address this issue, we analyzed the suboptimality of the policy obtained through maximizing discounted reward in relation to the policy that maximizes total reward and identified the influence of hyperparameters. Additionally, we proposed sufficient conditions for aligning the optimal policies of these two objectives under various settings. The primary contributions are as follows: We theoretically analyzed the factors influencing performance when using discounted reward as a proxy for total reward, thereby enhancing the theoretical understanding of this scenario. Furthermore, we developed methods to align the optimal policies of the two objectives in certain situations, which can improve the performance of reinforcement learning algorithms.

Probing Implicit Bias in Semi-gradient Q-learning: Visualizing the Effective Loss Landscapes via the Fokker--Planck Equation

Semi-gradient Q-learning is applied in many fields, but due to the absence of an explicit loss function, studying its dynamics and implicit bias in the parameter space is challenging. This paper introduces the Fokker--Planck equation and employs partial data obtained through sampling to construct and visualize the effective loss landscape within a two-dimensional parameter space. This visualization reveals how the global minima in the loss landscape can transform into saddle points in the effective loss landscape, as well as the implicit bias of the semi-gradient method. Additionally, we demonstrate that saddle points, originating from the global minima in loss landscape, still exist in the effective loss landscape under high-dimensional parameter spaces and neural network settings. This paper develop a novel approach for probing implicit bias in semi-gradient Q-learning.

A priori Estimates for Deep Residual Network in Continuous-time Reinforcement Learning

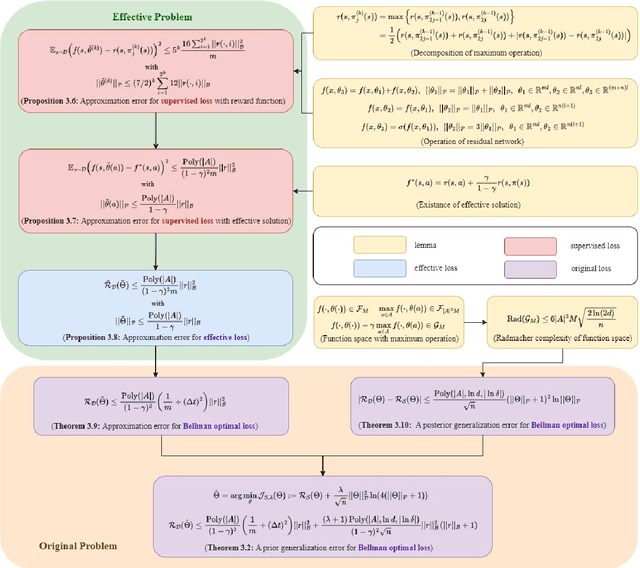
Deep reinforcement learning excels in numerous large-scale practical applications. However, existing performance analyses ignores the unique characteristics of continuous-time control problems, is unable to directly estimate the generalization error of the Bellman optimal loss and require a boundedness assumption. Our work focuses on continuous-time control problems and proposes a method that is applicable to all such problems where the transition function satisfies semi-group and Lipschitz properties. Under this method, we can directly analyze the \emph{a priori} generalization error of the Bellman optimal loss. The core of this method lies in two transformations of the loss function. To complete the transformation, we propose a decomposition method for the maximum operator. Additionally, this analysis method does not require a boundedness assumption. Finally, we obtain an \emph{a priori} generalization error without the curse of dimensionality.

An Experimental Comparison Between Temporal Difference and Residual Gradient with Neural Network Approximation

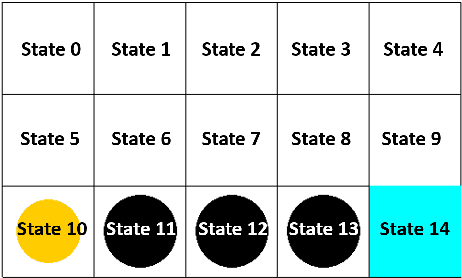
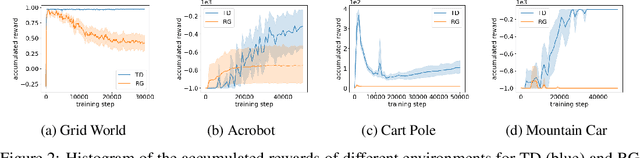
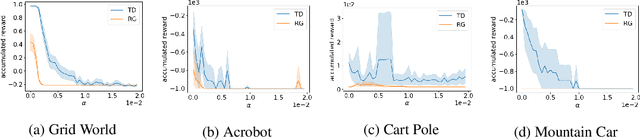
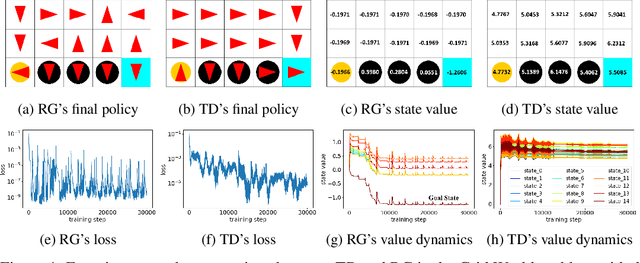
Gradient descent or its variants are popular in training neural networks. However, in deep Q-learning with neural network approximation, a type of reinforcement learning, gradient descent (also known as Residual Gradient (RG)) is barely used to solve Bellman residual minimization problem. On the contrary, Temporal Difference (TD), an incomplete gradient descent method prevails. In this work, we perform extensive experiments to show that TD outperforms RG, that is, when the training leads to a small Bellman residual error, the solution found by TD has a better policy and is more robust against the perturbation of neural network parameters. We further use experiments to reveal a key difference between reinforcement learning and supervised learning, that is, a small Bellman residual error can correspond to a bad policy in reinforcement learning while the test loss function in supervised learning is a standard index to indicate the performance. We also empirically examine that the missing term in TD is a key reason why RG performs badly. Our work shows that the performance of a deep Q-learning solution is closely related to the training dynamics and how an incomplete gradient descent method can find a good policy is interesting for future study.

FoldingZero: Protein Folding from Scratch in Hydrophobic-Polar Model

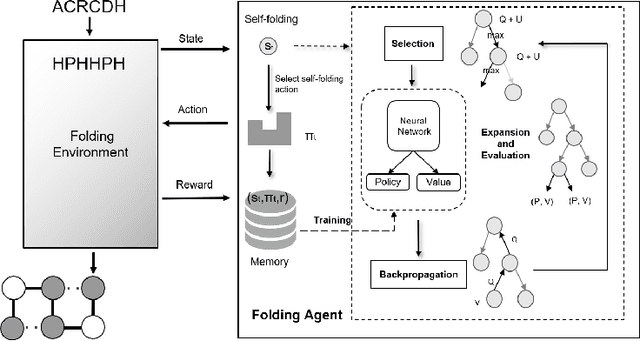
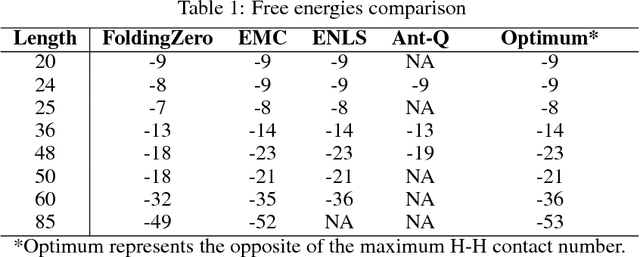
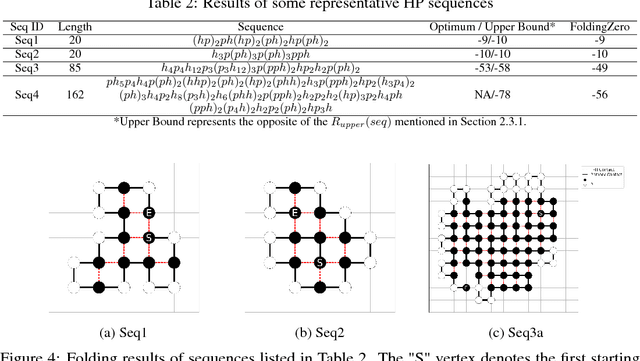
De novo protein structure prediction from amino acid sequence is one of the most challenging problems in computational biology. As one of the extensively explored mathematical models for protein folding, Hydrophobic-Polar (HP) model enables thorough investigation of protein structure formation and evolution. Although HP model discretizes the conformational space and simplifies the folding energy function, it has been proven to be an NP-complete problem. In this paper, we propose a novel protein folding framework FoldingZero, self-folding a de novo protein 2D HP structure from scratch based on deep reinforcement learning. FoldingZero features the coupled approach of a two-head (policy and value heads) deep convolutional neural network (HPNet) and a regularized Upper Confidence Bounds for Trees (R-UCT). It is trained solely by a reinforcement learning algorithm, which improves HPNet and R-UCT iteratively through iterative policy optimization. Without any supervision and domain knowledge, FoldingZero not only achieves comparable results, but also learns the latent folding knowledge to stabilize the structure. Without exponential computation, FoldingZero shows promising potential to be adopted for real-world protein properties prediction.