An Experimental Comparison Between Temporal Difference and Residual Gradient with Neural Network Approximation

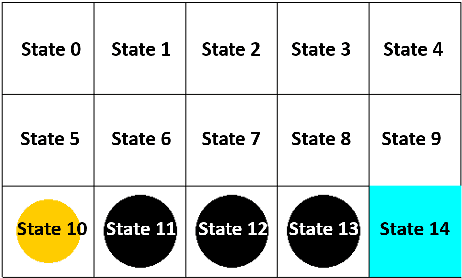
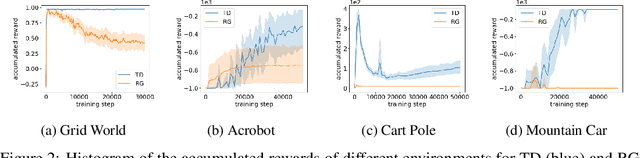
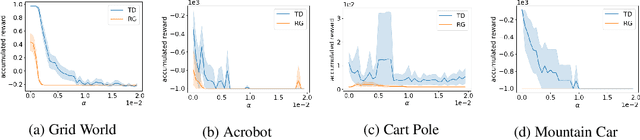
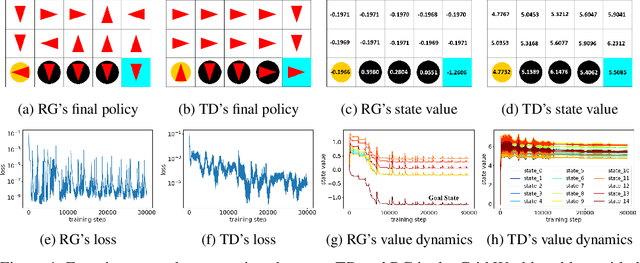
Gradient descent or its variants are popular in training neural networks. However, in deep Q-learning with neural network approximation, a type of reinforcement learning, gradient descent (also known as Residual Gradient (RG)) is barely used to solve Bellman residual minimization problem. On the contrary, Temporal Difference (TD), an incomplete gradient descent method prevails. In this work, we perform extensive experiments to show that TD outperforms RG, that is, when the training leads to a small Bellman residual error, the solution found by TD has a better policy and is more robust against the perturbation of neural network parameters. We further use experiments to reveal a key difference between reinforcement learning and supervised learning, that is, a small Bellman residual error can correspond to a bad policy in reinforcement learning while the test loss function in supervised learning is a standard index to indicate the performance. We also empirically examine that the missing term in TD is a key reason why RG performs badly. Our work shows that the performance of a deep Q-learning solution is closely related to the training dynamics and how an incomplete gradient descent method can find a good policy is interesting for future study.