A priori Estimates for Deep Residual Network in Continuous-time Reinforcement Learning
Paper and Code
Mar 07, 2024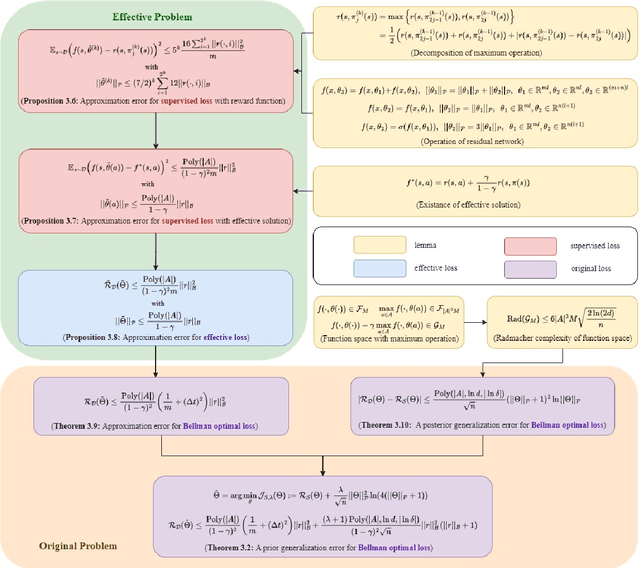
Deep reinforcement learning excels in numerous large-scale practical applications. However, existing performance analyses ignores the unique characteristics of continuous-time control problems, is unable to directly estimate the generalization error of the Bellman optimal loss and require a boundedness assumption. Our work focuses on continuous-time control problems and proposes a method that is applicable to all such problems where the transition function satisfies semi-group and Lipschitz properties. Under this method, we can directly analyze the \emph{a priori} generalization error of the Bellman optimal loss. The core of this method lies in two transformations of the loss function. To complete the transformation, we propose a decomposition method for the maximum operator. Additionally, this analysis method does not require a boundedness assumption. Finally, we obtain an \emph{a priori} generalization error without the curse of dimensionality.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge