Query-focused and Memory-aware Reranker for Long Context Processing

Built upon the existing analysis of retrieval heads in large language models, we propose an alternative reranking framework that trains models to estimate passage-query relevance using the attention scores of selected heads. This approach provides a listwise solution that leverages holistic information within the entire candidate shortlist during ranking. At the same time, it naturally produces continuous relevance scores, enabling training on arbitrary retrieval datasets without requiring Likert-scale supervision. Our framework is lightweight and effective, requiring only small-scale models (e.g., 4B parameters) to achieve strong performance. Extensive experiments demonstrate that our method outperforms existing state-of-the-art pointwise and listwise rerankers across multiple domains, including Wikipedia and long narrative datasets. It further establishes a new state-of-the-art on the LoCoMo benchmark that assesses the capabilities of dialogue understanding and memory usage. We further demonstrate that our framework supports flexible extensions. For example, augmenting candidate passages with contextual information further improves ranking accuracy, while training attention heads from middle layers enhances efficiency without sacrificing performance.

Multimodal Generative Retrieval Model with Staged Pretraining for Food Delivery on Meituan

Multimodal retrieval models are becoming increasingly important in scenarios such as food delivery, where rich multimodal features can meet diverse user needs and enable precise retrieval. Mainstream approaches typically employ a dual-tower architecture between queries and items, and perform joint optimization of intra-tower and inter-tower tasks. However, we observe that joint optimization often leads to certain modalities dominating the training process, while other modalities are neglected. In addition, inconsistent training speeds across modalities can easily result in the one-epoch problem. To address these challenges, we propose a staged pretraining strategy, which guides the model to focus on specialized tasks at each stage, enabling it to effectively attend to and utilize multimodal features, and allowing flexible control over the training process at each stage to avoid the one-epoch problem. Furthermore, to better utilize the semantic IDs that compress high-dimensional multimodal embeddings, we design both generative and discriminative tasks to help the model understand the associations between SIDs, queries, and item features, thereby improving overall performance. Extensive experiments on large-scale real-world Meituan data demonstrate that our method achieves improvements of 3.80%, 2.64%, and 2.17% on R@5, R@10, and R@20, and 5.10%, 4.22%, and 2.09% on N@5, N@10, and N@20 compared to mainstream baselines. Online A/B testing on the Meituan platform shows that our approach achieves a 1.12% increase in revenue and a 1.02% increase in click-through rate, validating the effectiveness and superiority of our method in practical applications.

ExDR: Explanation-driven Dynamic Retrieval Enhancement for Multimodal Fake News Detection

The rapid spread of multimodal fake news poses a serious societal threat, as its evolving nature and reliance on timely factual details challenge existing detection methods. Dynamic Retrieval-Augmented Generation provides a promising solution by triggering keyword-based retrieval and incorporating external knowledge, thus enabling both efficient and accurate evidence selection. However, it still faces challenges in addressing issues such as redundant retrieval, coarse similarity, and irrelevant evidence when applied to deceptive content. In this paper, we propose ExDR, an Explanation-driven Dynamic Retrieval-Augmented Generation framework for Multimodal Fake News Detection. Our framework systematically leverages model-generated explanations in both the retrieval triggering and evidence retrieval modules. It assesses triggering confidence from three complementary dimensions, constructs entity-aware indices by fusing deceptive entities, and retrieves contrastive evidence based on deception-specific features to challenge the initial claim and enhance the final prediction. Experiments on two benchmark datasets, AMG and MR2, demonstrate that ExDR consistently outperforms previous methods in retrieval triggering accuracy, retrieval quality, and overall detection performance, highlighting its effectiveness and generalization capability.

Mindscape-Aware Retrieval Augmented Generation for Improved Long Context Understanding

Humans understand long and complex texts by relying on a holistic semantic representation of the content. This global view helps organize prior knowledge, interpret new information, and integrate evidence dispersed across a document, as revealed by the Mindscape-Aware Capability of humans in psychology. Current Retrieval-Augmented Generation (RAG) systems lack such guidance and therefore struggle with long-context tasks. In this paper, we propose Mindscape-Aware RAG (MiA-RAG), the first approach that equips LLM-based RAG systems with explicit global context awareness. MiA-RAG builds a mindscape through hierarchical summarization and conditions both retrieval and generation on this global semantic representation. This enables the retriever to form enriched query embeddings and the generator to reason over retrieved evidence within a coherent global context. We evaluate MiA-RAG across diverse long-context and bilingual benchmarks for evidence-based understanding and global sense-making. It consistently surpasses baselines, and further analysis shows that it aligns local details with a coherent global representation, enabling more human-like long-context retrieval and reasoning.

The Stabilizer Bootstrap of Quantum Machine Learning with up to 10000 qubits

Quantum machine learning is considered one of the flagship applications of quantum computers, where variational quantum circuits could be the leading paradigm both in the near-term quantum devices and the early fault-tolerant quantum computers. However, it is not clear how to identify the regime of quantum advantages from these circuits, and there is no explicit theory to guide the practical design of variational ansatze to achieve better performance. We address these challenges with the stabilizer bootstrap, a method that uses stabilizer-based techniques to optimize quantum neural networks before their quantum execution, together with theoretical proofs and high-performance computing with 10000 qubits or random datasets up to 1000 data. We find that, in a general setup of variational ansatze, the possibility of improvements from the stabilizer bootstrap depends on the structure of the observables and the size of the datasets. The results reveal that configurations exhibit two distinct behaviors: some maintain a constant probability of circuit improvement, while others show an exponential decay in improvement probability as qubit numbers increase. These patterns are termed strong stabilizer enhancement and weak stabilizer enhancement, respectively, with most situations falling in between. Our work seamlessly bridges techniques from fault-tolerant quantum computing with applications of variational quantum algorithms. Not only does it offer practical insights for designing variational circuits tailored to large-scale machine learning challenges, but it also maps out a clear trajectory for defining the boundaries of feasible and practical quantum advantages.

Demystifying Lazy Training of Neural Networks from a Macroscopic Viewpoint

In this paper, we advance the understanding of neural network training dynamics by examining the intricate interplay of various factors introduced by weight parameters in the initialization process. Motivated by the foundational work of Luo et al. (J. Mach. Learn. Res., Vol. 22, Iss. 1, No. 71, pp 3327-3373), we explore the gradient descent dynamics of neural networks through the lens of macroscopic limits, where we analyze its behavior as width $m$ tends to infinity. Our study presents a unified approach with refined techniques designed for multi-layer fully connected neural networks, which can be readily extended to other neural network architectures. Our investigation reveals that gradient descent can rapidly drive deep neural networks to zero training loss, irrespective of the specific initialization schemes employed by weight parameters, provided that the initial scale of the output function $\kappa$ surpasses a certain threshold. This regime, characterized as the theta-lazy area, accentuates the predominant influence of the initial scale $\kappa$ over other factors on the training behavior of neural networks. Furthermore, our approach draws inspiration from the Neural Tangent Kernel (NTK) paradigm, and we expand its applicability. While NTK typically assumes that $\lim_{m\to\infty}\frac{\log \kappa}{\log m}=\frac{1}{2}$, and imposes each weight parameters to scale by the factor $\frac{1}{\sqrt{m}}$, in our theta-lazy regime, we discard the factor and relax the conditions to $\lim_{m\to\infty}\frac{\log \kappa}{\log m}>0$. Similar to NTK, the behavior of overparameterized neural networks within the theta-lazy regime trained by gradient descent can be effectively described by a specific kernel. Through rigorous analysis, our investigation illuminates the pivotal role of $\kappa$ in governing the training dynamics of neural networks.

Triple GNNs: Introducing Syntactic and Semantic Information for Conversational Aspect-Based Quadruple Sentiment Analysis

Conversational Aspect-Based Sentiment Analysis (DiaASQ) aims to detect quadruples \{target, aspect, opinion, sentiment polarity\} from given dialogues. In DiaASQ, elements constituting these quadruples are not necessarily confined to individual sentences but may span across multiple utterances within a dialogue. This necessitates a dual focus on both the syntactic information of individual utterances and the semantic interaction among them. However, previous studies have primarily focused on coarse-grained relationships between utterances, thus overlooking the potential benefits of detailed intra-utterance syntactic information and the granularity of inter-utterance relationships. This paper introduces the Triple GNNs network to enhance DiaAsQ. It employs a Graph Convolutional Network (GCN) for modeling syntactic dependencies within utterances and a Dual Graph Attention Network (DualGATs) to construct interactions between utterances. Experiments on two standard datasets reveal that our model significantly outperforms state-of-the-art baselines. The code is available at \url{https://github.com/nlperi2b/Triple-GNNs-}.

AC-EVAL: Evaluating Ancient Chinese Language Understanding in Large Language Models

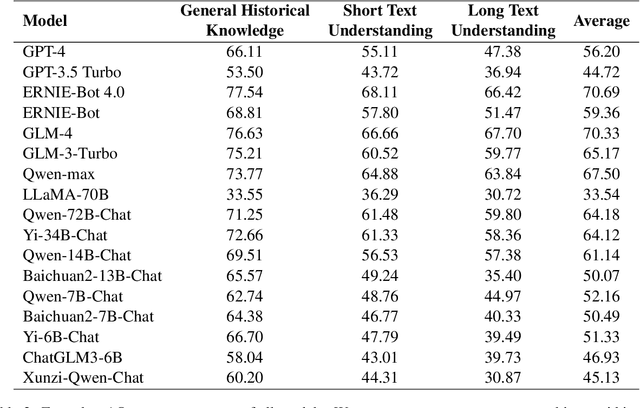
Given the importance of ancient Chinese in capturing the essence of rich historical and cultural heritage, the rapid advancements in Large Language Models (LLMs) necessitate benchmarks that can effectively evaluate their understanding of ancient contexts. To meet this need, we present AC-EVAL, an innovative benchmark designed to assess the advanced knowledge and reasoning capabilities of LLMs within the context of ancient Chinese. AC-EVAL is structured across three levels of difficulty reflecting different facets of language comprehension: general historical knowledge, short text understanding, and long text comprehension. The benchmark comprises 13 tasks, spanning historical facts, geography, social customs, art, philosophy, classical poetry and prose, providing a comprehensive assessment framework. Our extensive evaluation of top-performing LLMs, tailored for both English and Chinese, reveals a substantial potential for enhancing ancient text comprehension. By highlighting the strengths and weaknesses of LLMs, AC-EVAL aims to promote their development and application forward in the realms of ancient Chinese language education and scholarly research. The AC-EVAL data and evaluation code are available at https://github.com/yuting-wei/AC-EVAL.

Dynamic Multi-Scale Context Aggregation for Conversational Aspect-Based Sentiment Quadruple Analysis

Conversational aspect-based sentiment quadruple analysis (DiaASQ) aims to extract the quadruple of target-aspect-opinion-sentiment within a dialogue. In DiaASQ, a quadruple's elements often cross multiple utterances. This situation complicates the extraction process, emphasizing the need for an adequate understanding of conversational context and interactions. However, existing work independently encodes each utterance, thereby struggling to capture long-range conversational context and overlooking the deep inter-utterance dependencies. In this work, we propose a novel Dynamic Multi-scale Context Aggregation network (DMCA) to address the challenges. Specifically, we first utilize dialogue structure to generate multi-scale utterance windows for capturing rich contextual information. After that, we design a Dynamic Hierarchical Aggregation module (DHA) to integrate progressive cues between them. In addition, we form a multi-stage loss strategy to improve model performance and generalization ability. Extensive experimental results show that the DMCA model outperforms baselines significantly and achieves state-of-the-art performance.

Stochastic Modified Equations and Dynamics of Dropout Algorithm

Dropout is a widely utilized regularization technique in the training of neural networks, nevertheless, its underlying mechanism and its impact on achieving good generalization abilities remain poorly understood. In this work, we derive the stochastic modified equations for analyzing the dynamics of dropout, where its discrete iteration process is approximated by a class of stochastic differential equations. In order to investigate the underlying mechanism by which dropout facilitates the identification of flatter minima, we study the noise structure of the derived stochastic modified equation for dropout. By drawing upon the structural resemblance between the Hessian and covariance through several intuitive approximations, we empirically demonstrate the universal presence of the inverse variance-flatness relation and the Hessian-variance relation, throughout the training process of dropout. These theoretical and empirical findings make a substantial contribution to our understanding of the inherent tendency of dropout to locate flatter minima.