Santiago Zazo
CausalKANs: interpretable treatment effect estimation with Kolmogorov-Arnold networks
Sep 26, 2025Abstract:Deep neural networks achieve state-of-the-art performance in estimating heterogeneous treatment effects, but their opacity limits trust and adoption in sensitive domains such as medicine, economics, and public policy. Building on well-established and high-performing causal neural architectures, we propose causalKANs, a framework that transforms neural estimators of conditional average treatment effects (CATEs) into Kolmogorov--Arnold Networks (KANs). By incorporating pruning and symbolic simplification, causalKANs yields interpretable closed-form formulas while preserving predictive accuracy. Experiments on benchmark datasets demonstrate that causalKANs perform on par with neural baselines in CATE error metrics, and that even simple KAN variants achieve competitive performance, offering a favorable accuracy--interpretability trade-off. By combining reliability with analytic accessibility, causalKANs provide auditable estimators supported by closed-form expressions and interpretable plots, enabling trustworthy individualized decision-making in high-stakes settings. We release the code for reproducibility at https://github.com/aalmodovares/causalkans .
Deep Survival Analysis in Multimodal Medical Data: A Parametric and Probabilistic Approach with Competing Risks
Jul 10, 2025Abstract:Accurate survival prediction is critical in oncology for prognosis and treatment planning. Traditional approaches often rely on a single data modality, limiting their ability to capture the complexity of tumor biology. To address this challenge, we introduce a multimodal deep learning framework for survival analysis capable of modeling both single and competing risks scenarios, evaluating the impact of integrating multiple medical data sources on survival predictions. We propose SAMVAE (Survival Analysis Multimodal Variational Autoencoder), a novel deep learning architecture designed for survival prediction that integrates six data modalities: clinical variables, four molecular profiles, and histopathological images. SAMVAE leverages modality specific encoders to project inputs into a shared latent space, enabling robust survival prediction while preserving modality specific information. Its parametric formulation enables the derivation of clinically meaningful statistics from the output distributions, providing patient-specific insights through interactive multimedia that contribute to more informed clinical decision-making and establish a foundation for interpretable, data-driven survival analysis in oncology. We evaluate SAMVAE on two cancer cohorts breast cancer and lower grade glioma applying tailored preprocessing, dimensionality reduction, and hyperparameter optimization. The results demonstrate the successful integration of multimodal data for both standard survival analysis and competing risks scenarios across different datasets. Our model achieves competitive performance compared to state-of-the-art multimodal survival models. Notably, this is the first parametric multimodal deep learning architecture to incorporate competing risks while modeling continuous time to a specific event, using both tabular and image data.
DeCaFlow: A Deconfounding Causal Generative Model
Mar 19, 2025Abstract:Causal generative models (CGMs) have recently emerged as capable approaches to simulate the causal mechanisms generating our observations, enabling causal inference. Unfortunately, existing approaches either are overly restrictive, assuming the absence of hidden confounders, or lack generality, being tailored to a particular query and graph. In this work, we introduce DeCaFlow, a CGM that accounts for hidden confounders in a single amortized training process using only observational data and the causal graph. Importantly, DeCaFlow can provably identify all causal queries with a valid adjustment set or sufficiently informative proxy variables. Remarkably, for the first time to our knowledge, we show that a confounded counterfactual query is identifiable, and thus solvable by DeCaFlow, as long as its interventional counterpart is as well. Our empirical results on diverse settings (including the Ecoli70 dataset, with 3 independent hidden confounders, tens of observed variables and hundreds of causal queries) show that DeCaFlow outperforms existing approaches, while demonstrating its out-of-the-box flexibility.
Artificial Inductive Bias for Synthetic Tabular Data Generation in Data-Scarce Scenarios
Jul 03, 2024Abstract:While synthetic tabular data generation using Deep Generative Models (DGMs) offers a compelling solution to data scarcity and privacy concerns, their effectiveness relies on substantial training data, often unavailable in real-world applications. This paper addresses this challenge by proposing a novel methodology for generating realistic and reliable synthetic tabular data with DGMs in limited real-data environments. Our approach proposes several ways to generate an artificial inductive bias in a DGM through transfer learning and meta-learning techniques. We explore and compare four different methods within this framework, demonstrating that transfer learning strategies like pre-training and model averaging outperform meta-learning approaches, like Model-Agnostic Meta-Learning, and Domain Randomized Search. We validate our approach using two state-of-the-art DGMs, namely, a Variational Autoencoder and a Generative Adversarial Network, to show that our artificial inductive bias fuels superior synthetic data quality, as measured by Jensen-Shannon divergence, achieving relative gains of up to 50\% when using our proposed approach. This methodology has broad applicability in various DGMs and machine learning tasks, particularly in areas like healthcare and finance, where data scarcity is often a critical issue.
Synthetic Tabular Data Validation: A Divergence-Based Approach
May 13, 2024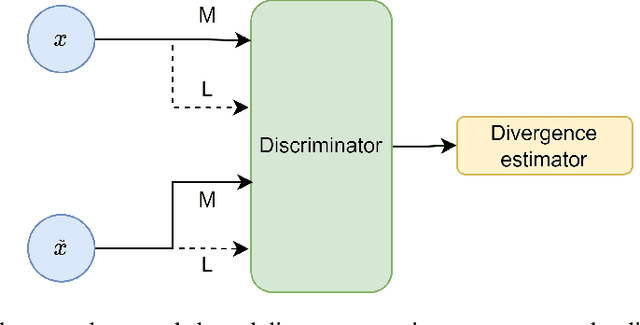


Abstract:The ever-increasing use of generative models in various fields where tabular data is used highlights the need for robust and standardized validation metrics to assess the similarity between real and synthetic data. Current methods lack a unified framework and rely on diverse and often inconclusive statistical measures. Divergences, which quantify discrepancies between data distributions, offer a promising avenue for validation. However, traditional approaches calculate divergences independently for each feature due to the complexity of joint distribution modeling. This paper addresses this challenge by proposing a novel approach that uses divergence estimation to overcome the limitations of marginal comparisons. Our core contribution lies in applying a divergence estimator to build a validation metric considering the joint distribution of real and synthetic data. We leverage a probabilistic classifier to approximate the density ratio between datasets, allowing the capture of complex relationships. We specifically calculate two divergences: the well-known Kullback-Leibler (KL) divergence and the Jensen-Shannon (JS) divergence. KL divergence offers an established use in the field, while JS divergence is symmetric and bounded, providing a reliable metric. The efficacy of this approach is demonstrated through a series of experiments with varying distribution complexities. The initial phase involves comparing estimated divergences with analytical solutions for simple distributions, setting a benchmark for accuracy. Finally, we validate our method on a real-world dataset and its corresponding synthetic counterpart, showcasing its effectiveness in practical applications. This research offers a significant contribution with applicability beyond tabular data and the potential to improve synthetic data validation in various fields.
An improved tabular data generator with VAE-GMM integration
Apr 12, 2024



Abstract:The rising use of machine learning in various fields requires robust methods to create synthetic tabular data. Data should preserve key characteristics while addressing data scarcity challenges. Current approaches based on Generative Adversarial Networks, such as the state-of-the-art CTGAN model, struggle with the complex structures inherent in tabular data. These data often contain both continuous and discrete features with non-Gaussian distributions. Therefore, we propose a novel Variational Autoencoder (VAE)-based model that addresses these limitations. Inspired by the TVAE model, our approach incorporates a Bayesian Gaussian Mixture model (BGM) within the VAE architecture. This avoids the limitations imposed by assuming a strictly Gaussian latent space, allowing for a more accurate representation of the underlying data distribution during data generation. Furthermore, our model offers enhanced flexibility by allowing the use of various differentiable distributions for individual features, making it possible to handle both continuous and discrete data types. We thoroughly validate our model on three real-world datasets with mixed data types, including two medically relevant ones, based on their resemblance and utility. This evaluation demonstrates significant outperformance against CTGAN and TVAE, establishing its potential as a valuable tool for generating synthetic tabular data in various domains, particularly in healthcare.
SAVAE: Leveraging the variational Bayes autoencoder for survival analysis
Dec 22, 2023



Abstract:As in many fields of medical research, survival analysis has witnessed a growing interest in the application of deep learning techniques to model complex, high-dimensional, heterogeneous, incomplete, and censored medical data. Current methods often make assumptions about the relations between data that may not be valid in practice. In response, we introduce SAVAE (Survival Analysis Variational Autoencoder), a novel approach based on Variational Autoencoders. SAVAE contributes significantly to the field by introducing a tailored ELBO formulation for survival analysis, supporting various parametric distributions for covariates and survival time (as long as the log-likelihood is differentiable). It offers a general method that consistently performs well on various metrics, demonstrating robustness and stability through different experiments. Our proposal effectively estimates time-to-event, accounting for censoring, covariate interactions, and time-varying risk associations. We validate our model in diverse datasets, including genomic, clinical, and demographic data, with varying levels of censoring. This approach demonstrates competitive performance compared to state-of-the-art techniques, as assessed by the Concordance Index and the Integrated Brier Score. SAVAE also offers an interpretable model that parametrically models covariates and time. Moreover, its generative architecture facilitates further applications such as clustering, data imputation, and the generation of synthetic patient data through latent space inference from survival data.
Learning Parametric Closed-Loop Policies for Markov Potential Games
May 22, 2018
Abstract:Multiagent systems where agents interact among themselves and with a stochastic environment can be formalized as stochastic games. We study a subclass named Markov potential games (MPGs) that appear often in economic and engineering applications when the agents share a common resource. We consider MPGs with continuous state-action variables, coupled constraints and nonconvex rewards. Previous analysis followed a variational approach that is only valid for very simple cases (convex rewards, invertible dynamics, and no coupled constraints); or considered deterministic dynamics and provided open-loop (OL) analysis, studying strategies that consist in predefined action sequences, which are not optimal for stochastic environments. We present a closed-loop (CL) analysis for MPGs and consider parametric policies that depend on the current state. We provide easily verifiable, sufficient and necessary conditions for a stochastic game to be an MPG, even for complex parametric functions (e.g., deep neural networks); and show that a closed-loop Nash equilibrium (NE) can be found (or at least approximated) by solving a related optimal control problem (OCP). This is useful since solving an OCP--which is a single-objective problem--is usually much simpler than solving the original set of coupled OCPs that form the game--which is a multiobjective control problem. This is a considerable improvement over the previously standard approach for the CL analysis of MPGs, which gives no approximate solution if no NE belongs to the chosen parametric family, and which is practical only for simple parametric forms. We illustrate the theoretical contributions with an example by applying our approach to a noncooperative communications engineering game. We then solve the game with a deep reinforcement learning algorithm that learns policies that closely approximates an exact variational NE of the game.
Diff-DAC: Distributed Actor-Critic for Average Multitask Deep Reinforcement Learning
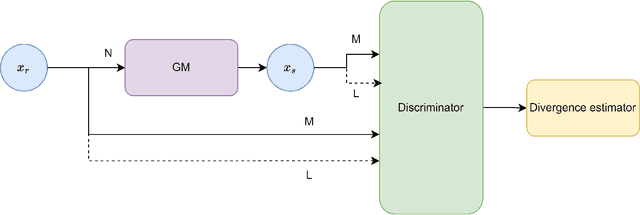
Apr 22, 2018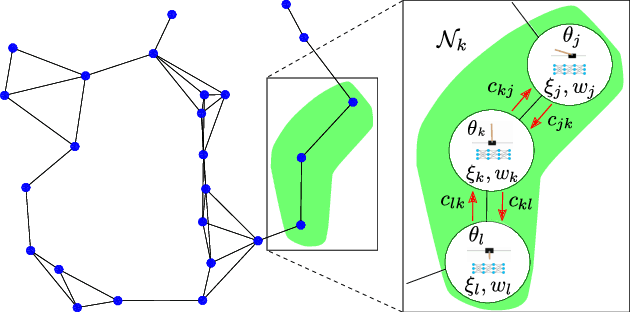
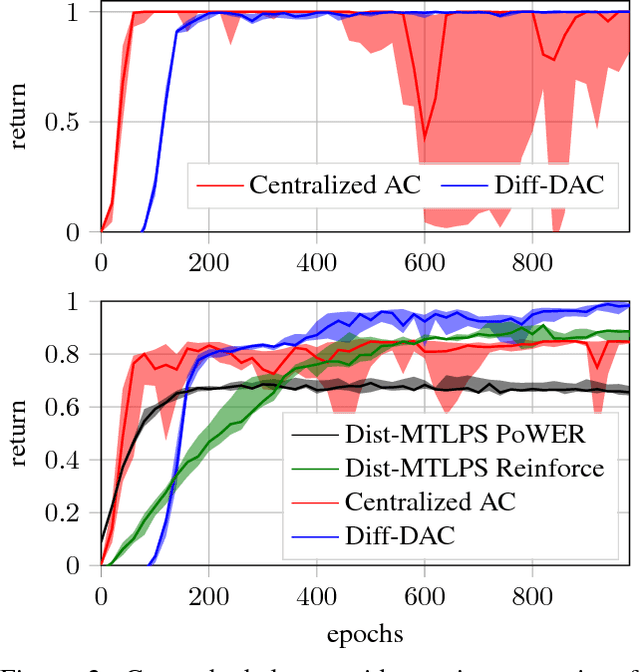
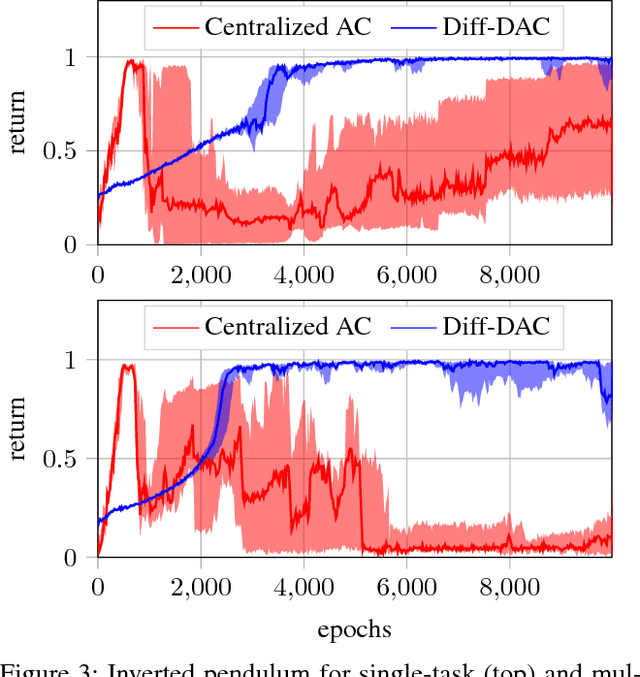
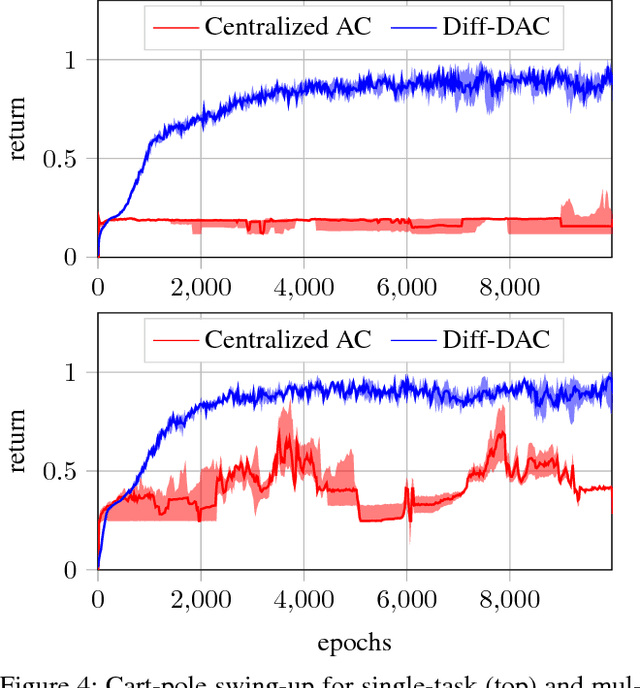
Abstract:We propose a fully distributed actor-critic algorithm approximated by deep neural networks, named \textit{Diff-DAC}, with application to single-task and to average multitask reinforcement learning (MRL). Each agent has access to data from its local task only, but it aims to learn a policy that performs well on average for the whole set of tasks. During the learning process, agents communicate their value-policy parameters to their neighbors, diffusing the information across the network, so that they converge to a common policy, with no need for a central node. The method is scalable, since the computational and communication costs per agent grow with its number of neighbors. We derive Diff-DAC's from duality theory and provide novel insights into the standard actor-critic framework, showing that it is actually an instance of the dual ascent method that approximates the solution of a linear program. Experiments suggest that Diff-DAC can outperform the single previous distributed MRL approach (i.e., Dist-MTLPS) and even the centralized architecture.
Distributed Policy Evaluation Under Multiple Behavior Strategies
Nov 05, 2014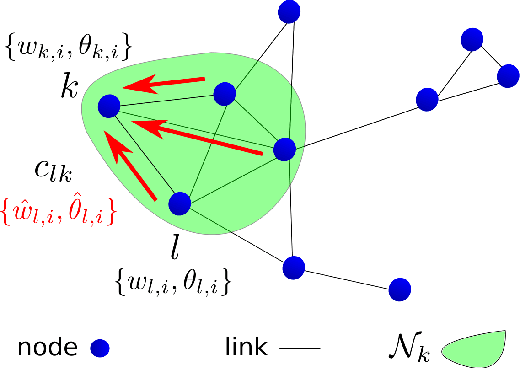
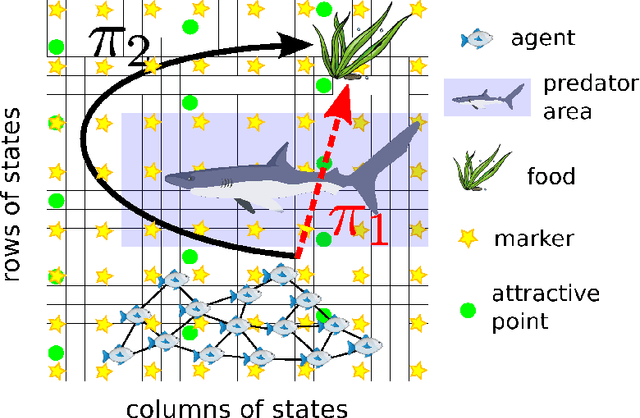
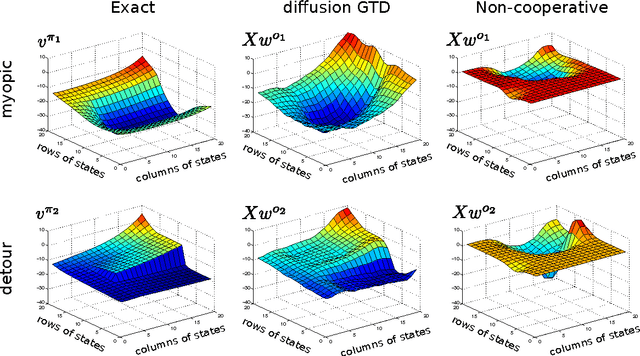
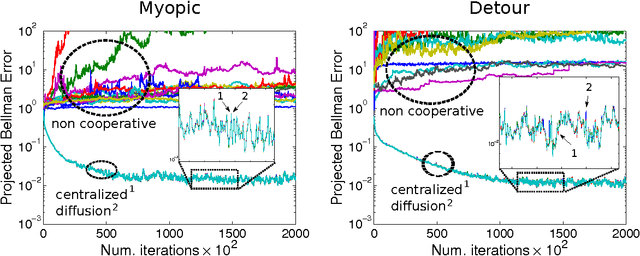
Abstract:We apply diffusion strategies to develop a fully-distributed cooperative reinforcement learning algorithm in which agents in a network communicate only with their immediate neighbors to improve predictions about their environment. The algorithm can also be applied to off-policy learning, meaning that the agents can predict the response to a behavior different from the actual policies they are following. The proposed distributed strategy is efficient, with linear complexity in both computation time and memory footprint. We provide a mean-square-error performance analysis and establish convergence under constant step-size updates, which endow the network with continuous learning capabilities. The results show a clear gain from cooperation: when the individual agents can estimate the solution, cooperation increases stability and reduces bias and variance of the prediction error; but, more importantly, the network is able to approach the optimal solution even when none of the individual agents can (e.g., when the individual behavior policies restrict each agent to sample a small portion of the state space).
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge