The Kernel Interaction Trick: Fast Bayesian Discovery of Pairwise Interactions in High Dimensions

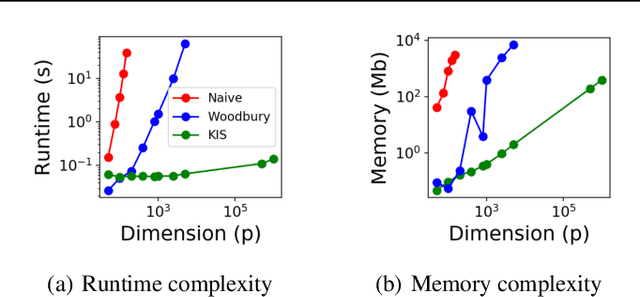
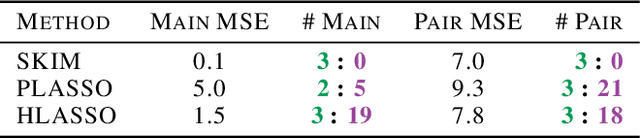
Discovering interaction effects on a response of interest is a fundamental problem faced in biology, medicine, economics, and many other scientific disciplines. In theory, Bayesian methods for discovering pairwise interactions enjoy many benefits such as coherent uncertainty quantification, the ability to incorporate background knowledge, and desirable shrinkage properties. In practice, however, Bayesian methods are often computationally intractable for even moderate-dimensional problems. Our key insight is that many hierarchical models of practical interest admit a particular Gaussian process (GP) representation; the GP allows us to capture the posterior with a vector of O(p) kernel hyper-parameters rather than O(p^2) interactions and main effects. With the implicit representation, we can run Markov chain Monte Carlo (MCMC) over model hyper-parameters in time and memory linear in p per iteration. We focus on sparsity-inducing models and show on datasets with a variety of covariate behaviors that our method: (1) reduces runtime by orders of magnitude over naive applications of MCMC, (2) provides lower Type I and Type II error relative to state-of-the-art LASSO-based approaches, and (3) offers improved computational scaling in high dimensions relative to existing Bayesian and LASSO-based approaches.

Overpruning in Variational Bayesian Neural Networks

The motivations for using variational inference (VI) in neural networks differ significantly from those in latent variable models. This has a counter-intuitive consequence; more expressive variational approximations can provide significantly worse predictions as compared to those with less expressive families. In this work we make two contributions. First, we identify a cause of this performance gap, variational over-pruning. Second, we introduce a theoretically grounded explanation for this phenomenon. Our perspective sheds light on several related published results and provides intuition into the design of effective variational approximations of neural networks.