Learning convolution operators on compact Abelian groups

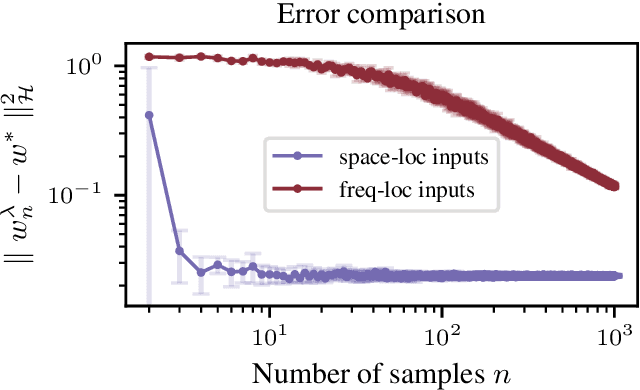
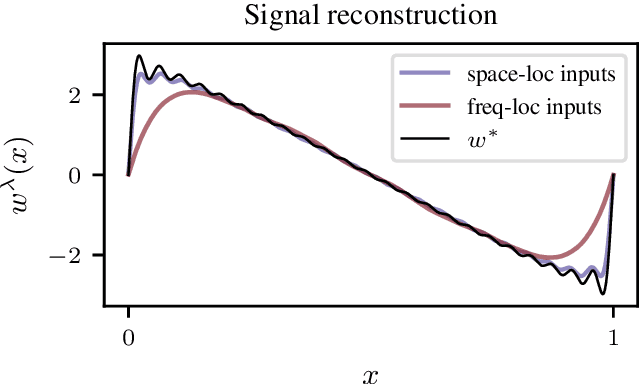
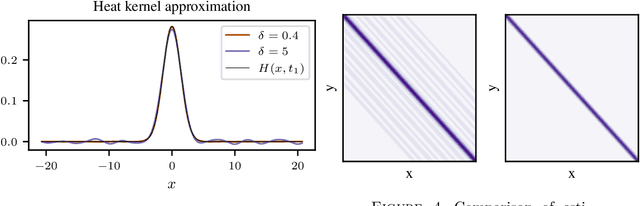
We consider the problem of learning convolution operators associated to compact Abelian groups. We study a regularization-based approach and provide corresponding learning guarantees, discussing natural regularity condition on the convolution kernel. More precisely, we assume the convolution kernel is a function in a translation invariant Hilbert space and analyze a natural ridge regression (RR) estimator. Building on existing results for RR, we characterize the accuracy of the estimator in terms of finite sample bounds. Interestingly, regularity assumptions which are classical in the analysis of RR, have a novel and natural interpretation in terms of space/frequency localization. Theoretical results are illustrated by numerical simulations.

Linearization Turns Neural Operators into Function-Valued Gaussian Processes

Modeling dynamical systems, e.g. in climate and engineering sciences, often necessitates solving partial differential equations. Neural operators are deep neural networks designed to learn nontrivial solution operators of such differential equations from data. As for all statistical models, the predictions of these models are imperfect and exhibit errors. Such errors are particularly difficult to spot in the complex nonlinear behaviour of dynamical systems. We introduce a new framework for approximate Bayesian uncertainty quantification in neural operators using function-valued Gaussian processes. Our approach can be interpreted as a probabilistic analogue of the concept of currying from functional programming and provides a practical yet theoretically sound way to apply the linearized Laplace approximation to neural operators. In a case study on Fourier neural operators, we show that, even for a discretized input, our method yields a Gaussian closure--a structured Gaussian process posterior capturing the uncertainty in the output function of the neural operator, which can be evaluated at an arbitrary set of points. The method adds minimal prediction overhead, can be applied post-hoc without retraining the neural operator, and scales to large models and datasets. We showcase the efficacy of our approach through applications to different types of partial differential equations.

Approximate Bayesian Neural Operators: Uncertainty Quantification for Parametric PDEs

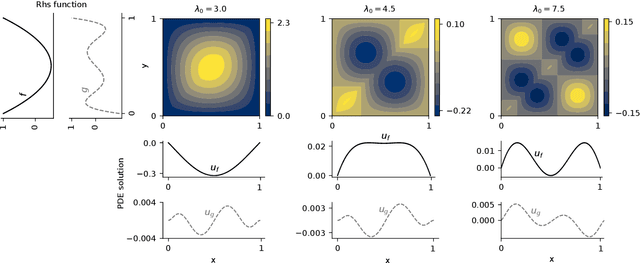
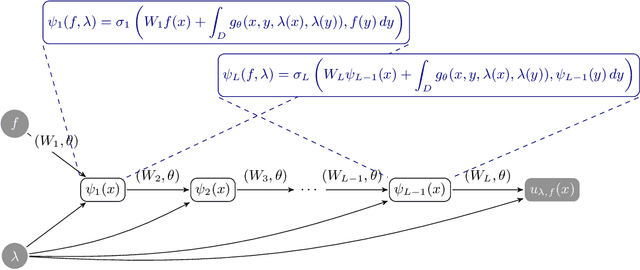
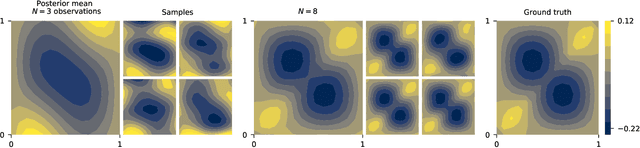
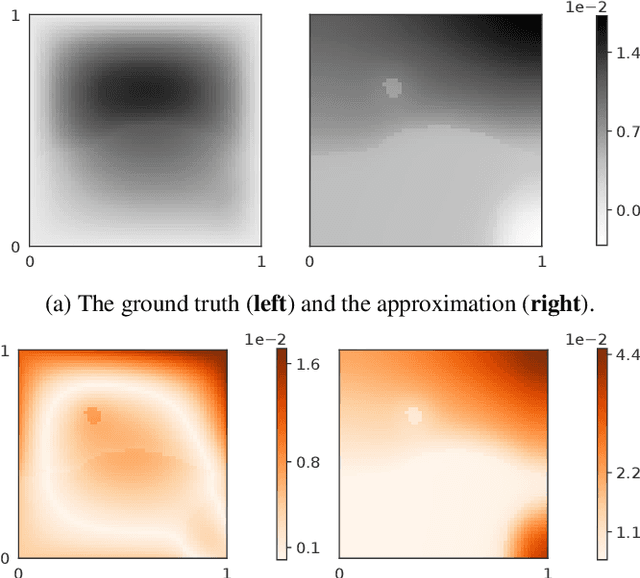
Neural operators are a type of deep architecture that learns to solve (i.e. learns the nonlinear solution operator of) partial differential equations (PDEs). The current state of the art for these models does not provide explicit uncertainty quantification. This is arguably even more of a problem for this kind of tasks than elsewhere in machine learning, because the dynamical systems typically described by PDEs often exhibit subtle, multiscale structure that makes errors hard to spot by humans. In this work, we first provide a mathematically detailed Bayesian formulation of the ''shallow'' (linear) version of neural operators in the formalism of Gaussian processes. We then extend this analytic treatment to general deep neural operators using approximate methods from Bayesian deep learning. We extend previous results on neural operators by providing them with uncertainty quantification. As a result, our approach is able to identify cases, and provide structured uncertainty estimates, where the neural operator fails to predict well.

Bayesian Filtering for ODEs with Bounded Derivatives

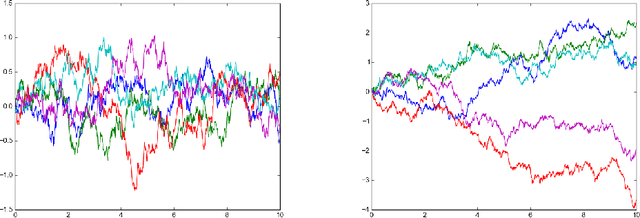
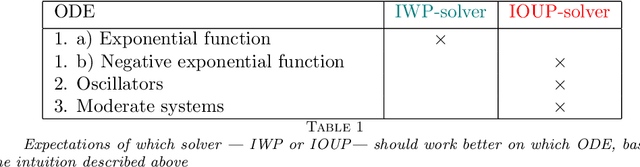
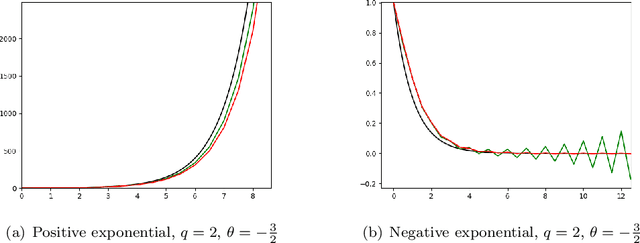
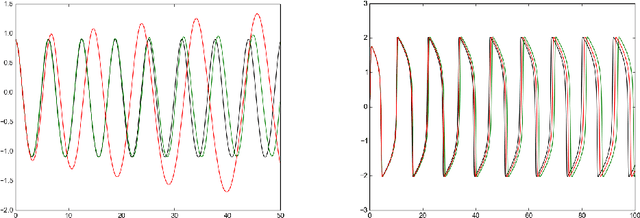
Recently there has been increasing interest in probabilistic solvers for ordinary differential equations (ODEs) that return full probability measures, instead of point estimates, over the solution and can incorporate uncertainty over the ODE at hand, e.g. if the vector field or the initial value is only approximately known or evaluable. The ODE filter proposed in recent work models the solution of the ODE by a Gauss-Markov process which serves as a prior in the sense of Bayesian statistics. While previous work employed a Wiener process prior on the (possibly multiple times) differentiated solution of the ODE and established equivalence of the corresponding solver with classical numerical methods, this paper raises the question whether other priors also yield practically useful solvers. To this end, we discuss a range of possible priors which enable fast filtering and propose a new prior--the Integrated Ornstein Uhlenbeck Process (IOUP)--that complements the existing Integrated Wiener process (IWP) filter by encoding the property that a derivative in time of the solution is bounded in the sense that it tends to drift back to zero. We provide experiments comparing IWP and IOUP filters which support the belief that IWP approximates better divergent ODE's solutions whereas IOUP is a better prior for trajectories with bounded derivatives.