Learning convolution operators on compact Abelian groups
Paper and Code
Jan 09, 2025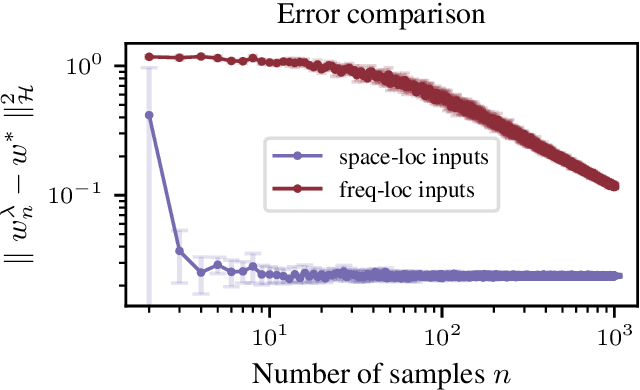
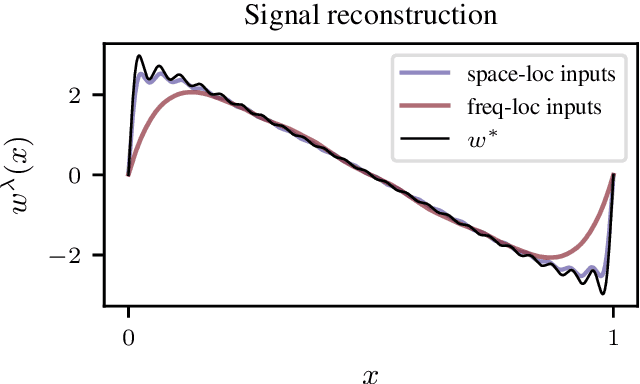
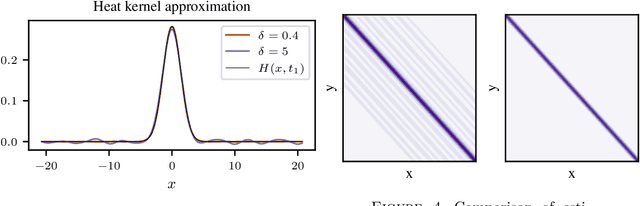
We consider the problem of learning convolution operators associated to compact Abelian groups. We study a regularization-based approach and provide corresponding learning guarantees, discussing natural regularity condition on the convolution kernel. More precisely, we assume the convolution kernel is a function in a translation invariant Hilbert space and analyze a natural ridge regression (RR) estimator. Building on existing results for RR, we characterize the accuracy of the estimator in terms of finite sample bounds. Interestingly, regularity assumptions which are classical in the analysis of RR, have a novel and natural interpretation in terms of space/frequency localization. Theoretical results are illustrated by numerical simulations.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge