Approximate Bayesian Neural Operators: Uncertainty Quantification for Parametric PDEs
Paper and Code
Aug 02, 2022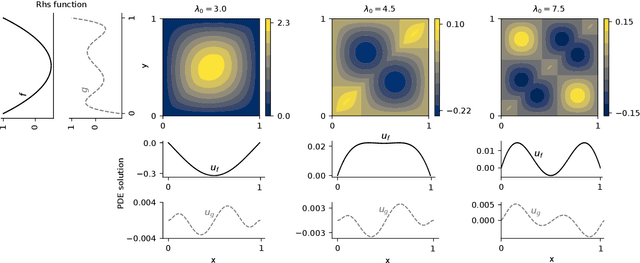
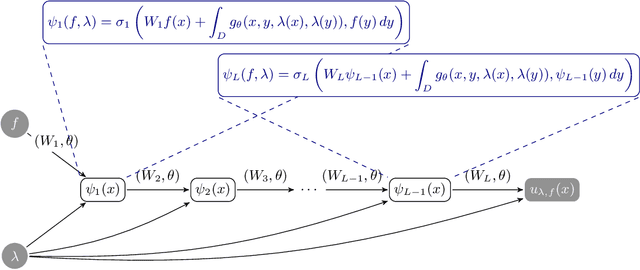
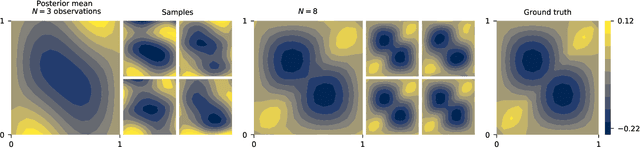

Neural operators are a type of deep architecture that learns to solve (i.e. learns the nonlinear solution operator of) partial differential equations (PDEs). The current state of the art for these models does not provide explicit uncertainty quantification. This is arguably even more of a problem for this kind of tasks than elsewhere in machine learning, because the dynamical systems typically described by PDEs often exhibit subtle, multiscale structure that makes errors hard to spot by humans. In this work, we first provide a mathematically detailed Bayesian formulation of the ''shallow'' (linear) version of neural operators in the formalism of Gaussian processes. We then extend this analytic treatment to general deep neural operators using approximate methods from Bayesian deep learning. We extend previous results on neural operators by providing them with uncertainty quantification. As a result, our approach is able to identify cases, and provide structured uncertainty estimates, where the neural operator fails to predict well.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge