How far away are truly hyperparameter-free learning algorithms?

Despite major advances in methodology, hyperparameter tuning remains a crucial (and expensive) part of the development of machine learning systems. Even ignoring architectural choices, deep neural networks have a large number of optimization and regularization hyperparameters that need to be tuned carefully per workload in order to obtain the best results. In a perfect world, training algorithms would not require workload-specific hyperparameter tuning, but would instead have default settings that performed well across many workloads. Recently, there has been a growing literature on optimization methods which attempt to reduce the number of hyperparameters -- particularly the learning rate and its accompanying schedule. Given these developments, how far away is the dream of neural network training algorithms that completely obviate the need for painful tuning? In this paper, we evaluate the potential of learning-rate-free methods as components of hyperparameter-free methods. We freeze their (non-learning rate) hyperparameters to default values, and score their performance using the recently-proposed AlgoPerf: Training Algorithms benchmark. We found that literature-supplied default settings performed poorly on the benchmark, so we performed a search for hyperparameter configurations that performed well across all workloads simultaneously. The best AlgoPerf-calibrated learning-rate-free methods had much improved performance but still lagged slightly behind a similarly calibrated NadamW baseline in overall benchmark score. Our results suggest that there is still much room for improvement for learning-rate-free methods, and that testing against a strong, workload-agnostic baseline is important to improve hyperparameter reduction techniques.

Learning by solving differential equations

Modern deep learning algorithms use variations of gradient descent as their main learning methods. Gradient descent can be understood as the simplest Ordinary Differential Equation (ODE) solver; namely, the Euler method applied to the gradient flow differential equation. Since Euler, many ODE solvers have been devised that follow the gradient flow equation more precisely and more stably. Runge-Kutta (RK) methods provide a family of very powerful explicit and implicit high-order ODE solvers. However, these higher-order solvers have not found wide application in deep learning so far. In this work, we evaluate the performance of higher-order RK solvers when applied in deep learning, study their limitations, and propose ways to overcome these drawbacks. In particular, we explore how to improve their performance by naturally incorporating key ingredients of modern neural network optimizers such as preconditioning, adaptive learning rates, and momentum.

Training neural networks faster with minimal tuning using pre-computed lists of hyperparameters for NAdamW

If we want to train a neural network using any of the most popular optimization algorithms, we are immediately faced with a dilemma: how to set the various optimization and regularization hyperparameters? When computational resources are abundant, there are a variety of methods for finding good hyperparameter settings, but when resources are limited the only realistic choices are using standard default values of uncertain quality and provenance, or tuning only a couple of the most important hyperparameters via extremely limited handdesigned sweeps. Extending the idea of default settings to a modest tuning budget, Metz et al. (2020) proposed using ordered lists of well-performing hyperparameter settings, derived from a broad hyperparameter search on a large library of training workloads. However, to date, no practical and performant hyperparameter lists that generalize to representative deep learning workloads have been demonstrated. In this paper, we present hyperparameter lists for NAdamW derived from extensive experiments on the realistic workloads in the AlgoPerf: Training Algorithms benchmark. Our hyperparameter lists also include values for basic regularization techniques (i.e. weight decay, label smoothing, and dropout). In particular, our best NAdamW hyperparameter list performs well on AlgoPerf held-out workloads not used to construct it, and represents a compelling turn-key approach to tuning when restricted to five or fewer trials. It also outperforms basic learning rate/weight decay sweeps and an off-the-shelf Bayesian optimization tool when restricted to the same budget.

Accelerating Neural Network Training: An Analysis of the AlgoPerf Competition

The goal of the AlgoPerf: Training Algorithms competition is to evaluate practical speed-ups in neural network training achieved solely by improving the underlying training algorithms. In the external tuning ruleset, submissions must provide workload-agnostic hyperparameter search spaces, while in the self-tuning ruleset they must be completely hyperparameter-free. In both rulesets, submissions are compared on time-to-result across multiple deep learning workloads, training on fixed hardware. This paper presents the inaugural AlgoPerf competition's results, which drew 18 diverse submissions from 10 teams. Our investigation reveals several key findings: (1) The winning submission in the external tuning ruleset, using Distributed Shampoo, demonstrates the effectiveness of non-diagonal preconditioning over popular methods like Adam, even when compared on wall-clock runtime. (2) The winning submission in the self-tuning ruleset, based on the Schedule Free AdamW algorithm, demonstrates a new level of effectiveness for completely hyperparameter-free training algorithms. (3) The top-scoring submissions were surprisingly robust to workload changes. We also discuss the engineering challenges encountered in ensuring a fair comparison between different training algorithms. These results highlight both the significant progress so far, and the considerable room for further improvements.

Towards flexible perception with visual memory

Training a neural network is a monolithic endeavor, akin to carving knowledge into stone: once the process is completed, editing the knowledge in a network is nearly impossible, since all information is distributed across the network's weights. We here explore a simple, compelling alternative by marrying the representational power of deep neural networks with the flexibility of a database. Decomposing the task of image classification into image similarity (from a pre-trained embedding) and search (via fast nearest neighbor retrieval from a knowledge database), we build a simple and flexible visual memory that has the following key capabilities: (1.) The ability to flexibly add data across scales: from individual samples all the way to entire classes and billion-scale data; (2.) The ability to remove data through unlearning and memory pruning; (3.) An interpretable decision-mechanism on which we can intervene to control its behavior. Taken together, these capabilities comprehensively demonstrate the benefits of an explicit visual memory. We hope that it might contribute to a conversation on how knowledge should be represented in deep vision models -- beyond carving it in ``stone'' weights.

Grandmaster-Level Chess Without Search

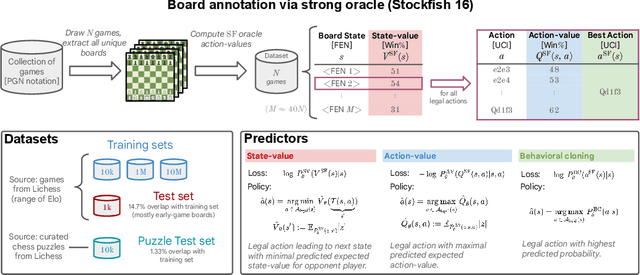
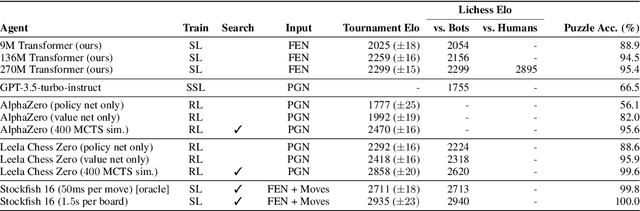
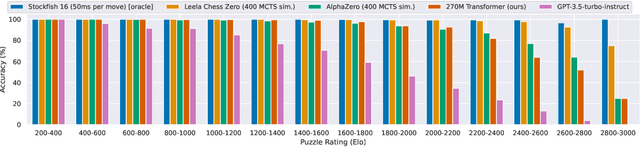
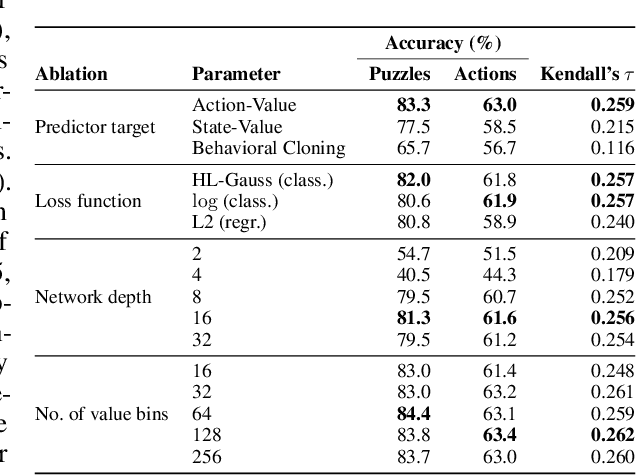
The recent breakthrough successes in machine learning are mainly attributed to scale: namely large-scale attention-based architectures and datasets of unprecedented scale. This paper investigates the impact of training at scale for chess. Unlike traditional chess engines that rely on complex heuristics, explicit search, or a combination of both, we train a 270M parameter transformer model with supervised learning on a dataset of 10 million chess games. We annotate each board in the dataset with action-values provided by the powerful Stockfish 16 engine, leading to roughly 15 billion data points. Our largest model reaches a Lichess blitz Elo of 2895 against humans, and successfully solves a series of challenging chess puzzles, without any domain-specific tweaks or explicit search algorithms. We also show that our model outperforms AlphaZero's policy and value networks (without MCTS) and GPT-3.5-turbo-instruct. A systematic investigation of model and dataset size shows that strong chess performance only arises at sufficient scale. To validate our results, we perform an extensive series of ablations of design choices and hyperparameters.

Benchmarking Neural Network Training Algorithms

Training algorithms, broadly construed, are an essential part of every deep learning pipeline. Training algorithm improvements that speed up training across a wide variety of workloads (e.g., better update rules, tuning protocols, learning rate schedules, or data selection schemes) could save time, save computational resources, and lead to better, more accurate, models. Unfortunately, as a community, we are currently unable to reliably identify training algorithm improvements, or even determine the state-of-the-art training algorithm. In this work, using concrete experiments, we argue that real progress in speeding up training requires new benchmarks that resolve three basic challenges faced by empirical comparisons of training algorithms: (1) how to decide when training is complete and precisely measure training time, (2) how to handle the sensitivity of measurements to exact workload details, and (3) how to fairly compare algorithms that require hyperparameter tuning. In order to address these challenges, we introduce a new, competitive, time-to-result benchmark using multiple workloads running on fixed hardware, the AlgoPerf: Training Algorithms benchmark. Our benchmark includes a set of workload variants that make it possible to detect benchmark submissions that are more robust to workload changes than current widely-used methods. Finally, we evaluate baseline submissions constructed using various optimizers that represent current practice, as well as other optimizers that have recently received attention in the literature. These baseline results collectively demonstrate the feasibility of our benchmark, show that non-trivial gaps between methods exist, and set a provisional state-of-the-art for future benchmark submissions to try and surpass.

Adaptive Gradient Methods at the Edge of Stability

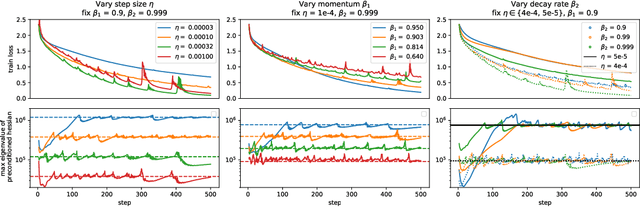
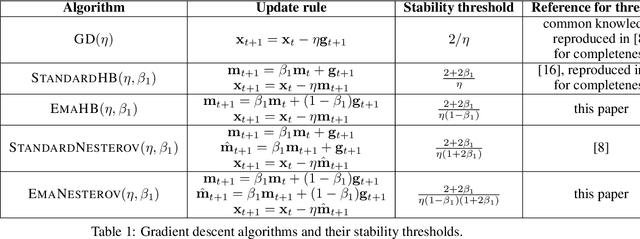
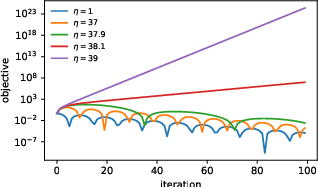
Very little is known about the training dynamics of adaptive gradient methods like Adam in deep learning. In this paper, we shed light on the behavior of these algorithms in the full-batch and sufficiently large batch settings. Specifically, we empirically demonstrate that during full-batch training, the maximum eigenvalue of the preconditioned Hessian typically equilibrates at a certain numerical value -- the stability threshold of a gradient descent algorithm. For Adam with step size $\eta$ and $\beta_1 = 0.9$, this stability threshold is $38/\eta$. Similar effects occur during minibatch training, especially as the batch size grows. Yet, even though adaptive methods train at the ``Adaptive Edge of Stability'' (AEoS), their behavior in this regime differs in a significant way from that of non-adaptive methods at the EoS. Whereas non-adaptive algorithms at the EoS are blocked from entering high-curvature regions of the loss landscape, adaptive gradient methods at the AEoS can keep advancing into high-curvature regions, while adapting the preconditioner to compensate. Our findings can serve as a foundation for the community's future understanding of adaptive gradient methods in deep learning.