Benchmarking Neural Network Training Algorithms

Training algorithms, broadly construed, are an essential part of every deep learning pipeline. Training algorithm improvements that speed up training across a wide variety of workloads (e.g., better update rules, tuning protocols, learning rate schedules, or data selection schemes) could save time, save computational resources, and lead to better, more accurate, models. Unfortunately, as a community, we are currently unable to reliably identify training algorithm improvements, or even determine the state-of-the-art training algorithm. In this work, using concrete experiments, we argue that real progress in speeding up training requires new benchmarks that resolve three basic challenges faced by empirical comparisons of training algorithms: (1) how to decide when training is complete and precisely measure training time, (2) how to handle the sensitivity of measurements to exact workload details, and (3) how to fairly compare algorithms that require hyperparameter tuning. In order to address these challenges, we introduce a new, competitive, time-to-result benchmark using multiple workloads running on fixed hardware, the AlgoPerf: Training Algorithms benchmark. Our benchmark includes a set of workload variants that make it possible to detect benchmark submissions that are more robust to workload changes than current widely-used methods. Finally, we evaluate baseline submissions constructed using various optimizers that represent current practice, as well as other optimizers that have recently received attention in the literature. These baseline results collectively demonstrate the feasibility of our benchmark, show that non-trivial gaps between methods exist, and set a provisional state-of-the-art for future benchmark submissions to try and surpass.

Adaptive Gradient Methods at the Edge of Stability

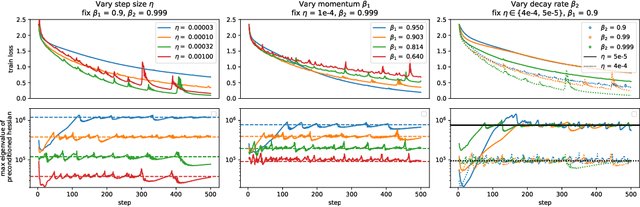
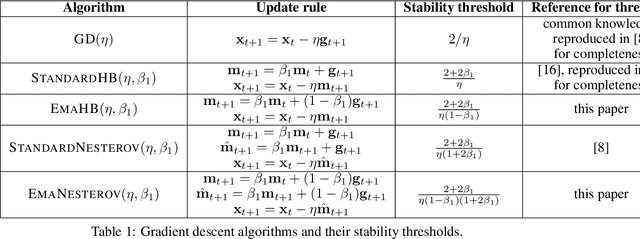
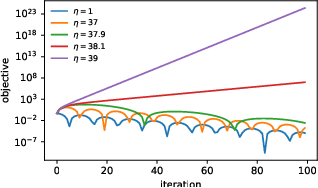
Very little is known about the training dynamics of adaptive gradient methods like Adam in deep learning. In this paper, we shed light on the behavior of these algorithms in the full-batch and sufficiently large batch settings. Specifically, we empirically demonstrate that during full-batch training, the maximum eigenvalue of the preconditioned Hessian typically equilibrates at a certain numerical value -- the stability threshold of a gradient descent algorithm. For Adam with step size $\eta$ and $\beta_1 = 0.9$, this stability threshold is $38/\eta$. Similar effects occur during minibatch training, especially as the batch size grows. Yet, even though adaptive methods train at the ``Adaptive Edge of Stability'' (AEoS), their behavior in this regime differs in a significant way from that of non-adaptive methods at the EoS. Whereas non-adaptive algorithms at the EoS are blocked from entering high-curvature regions of the loss landscape, adaptive gradient methods at the AEoS can keep advancing into high-curvature regions, while adapting the preconditioner to compensate. Our findings can serve as a foundation for the community's future understanding of adaptive gradient methods in deep learning.