Adaptive Gradient Methods at the Edge of Stability

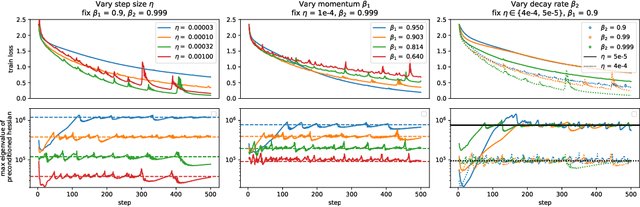
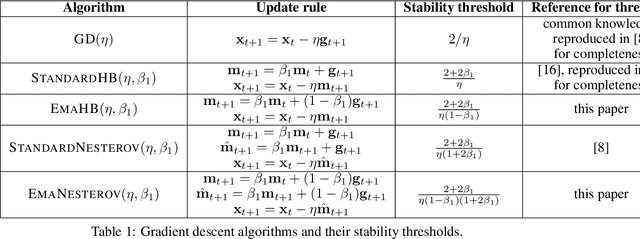
Very little is known about the training dynamics of adaptive gradient methods like Adam in deep learning. In this paper, we shed light on the behavior of these algorithms in the full-batch and sufficiently large batch settings. Specifically, we empirically demonstrate that during full-batch training, the maximum eigenvalue of the preconditioned Hessian typically equilibrates at a certain numerical value -- the stability threshold of a gradient descent algorithm. For Adam with step size $\eta$ and $\beta_1 = 0.9$, this stability threshold is $38/\eta$. Similar effects occur during minibatch training, especially as the batch size grows. Yet, even though adaptive methods train at the ``Adaptive Edge of Stability'' (AEoS), their behavior in this regime differs in a significant way from that of non-adaptive methods at the EoS. Whereas non-adaptive algorithms at the EoS are blocked from entering high-curvature regions of the loss landscape, adaptive gradient methods at the AEoS can keep advancing into high-curvature regions, while adapting the preconditioner to compensate. Our findings can serve as a foundation for the community's future understanding of adaptive gradient methods in deep learning.

A Loss Curvature Perspective on Training Instability in Deep Learning

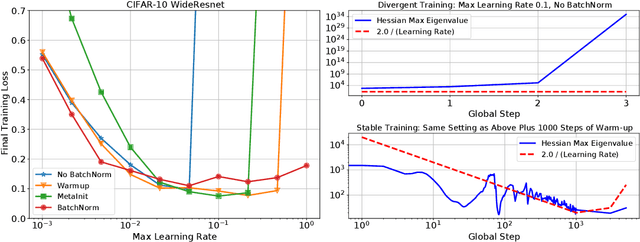
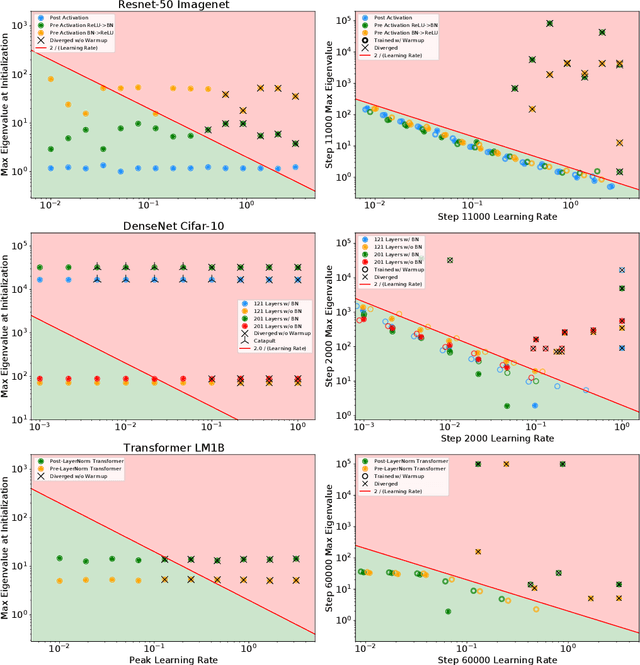
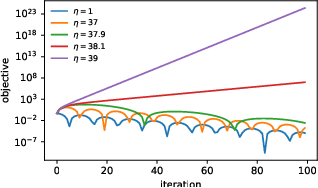
In this work, we study the evolution of the loss Hessian across many classification tasks in order to understand the effect the curvature of the loss has on the training dynamics. Whereas prior work has focused on how different learning rates affect the loss Hessian observed during training, we also analyze the effects of model initialization, architectural choices, and common training heuristics such as gradient clipping and learning rate warmup. Our results demonstrate that successful model and hyperparameter choices allow the early optimization trajectory to either avoid -- or navigate out of -- regions of high curvature and into flatter regions that tolerate a higher learning rate. Our results suggest a unifying perspective on how disparate mitigation strategies for training instability ultimately address the same underlying failure mode of neural network optimization, namely poor conditioning. Inspired by the conditioning perspective, we show that learning rate warmup can improve training stability just as much as batch normalization, layer normalization, MetaInit, GradInit, and Fixup initialization.