Accurate and Conservative Estimates of MRF Log-likelihood using Reverse Annealing

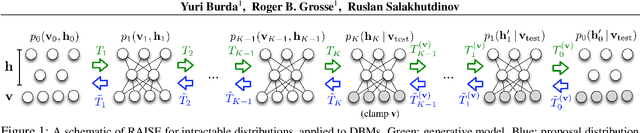
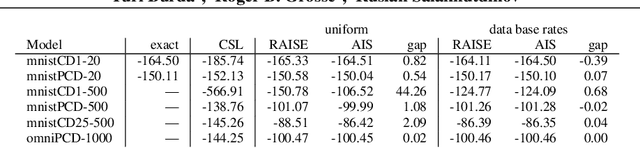
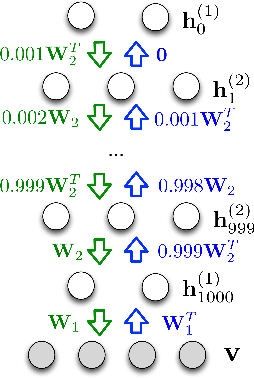
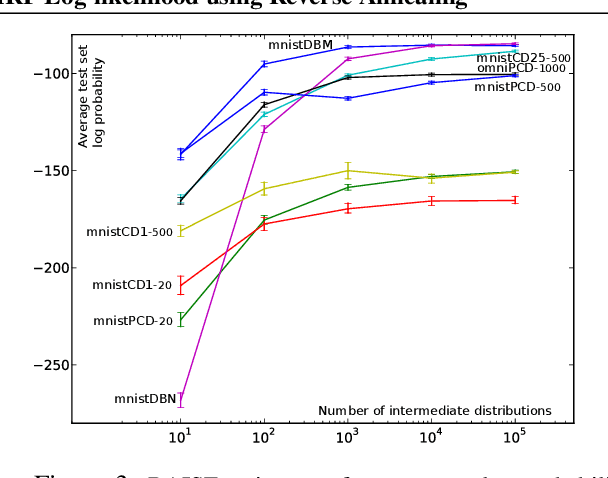
Markov random fields (MRFs) are difficult to evaluate as generative models because computing the test log-probabilities requires the intractable partition function. Annealed importance sampling (AIS) is widely used to estimate MRF partition functions, and often yields quite accurate results. However, AIS is prone to overestimate the log-likelihood with little indication that anything is wrong. We present the Reverse AIS Estimator (RAISE), a stochastic lower bound on the log-likelihood of an approximation to the original MRF model. RAISE requires only the same MCMC transition operators as standard AIS. Experimental results indicate that RAISE agrees closely with AIS log-probability estimates for RBMs, DBMs, and DBNs, but typically errs on the side of underestimating, rather than overestimating, the log-likelihood.