Understanding and Minimising Outlier Features in Neural Network Training

Outlier Features (OF) are neurons whose activation magnitudes significantly exceed the average over a neural network's (NN) width. They are well known to emerge during standard transformer training and have the undesirable effect of hindering quantisation in afflicted models. Despite their practical importance, little is known behind why OFs emerge during training, nor how one can minimise them. Our work focuses on the above questions, first identifying several quantitative metrics, such as the kurtosis over neuron activation norms, to measure OFs. With these metrics, we study how architectural and optimisation choices influence OFs, and provide practical insights to minimise OFs during training. As highlights, we emphasise the importance of controlling signal propagation throughout training, and propose the Outlier Protected transformer block, which removes standard Pre-Norm layers to mitigate OFs, without loss of convergence speed or training stability. Overall, our findings shed new light on our understanding of, our ability to prevent, and the complexity of this important facet in NN training dynamics.

Hallmarks of Optimization Trajectories in Neural Networks and LLMs: The Lengths, Bends, and Dead Ends

We propose a fresh take on understanding the mechanisms of neural networks by analyzing the rich structure of parameters contained within their optimization trajectories. Towards this end, we introduce some natural notions of the complexity of optimization trajectories, both qualitative and quantitative, which reveal the inherent nuance and interplay involved between various optimization choices, such as momentum, weight decay, and batch size. We use them to provide key hallmarks about the nature of optimization in deep neural networks: when it goes right, and when it finds itself in a dead end. Further, thanks to our trajectory perspective, we uncover an intertwined behaviour of momentum and weight decay that promotes directional exploration, as well as a directional regularization behaviour of some others. We perform experiments over large-scale vision and language settings, including large language models (LLMs) with up to 12 billion parameters, to demonstrate the value of our approach.

Recurrent Distance-Encoding Neural Networks for Graph Representation Learning

Graph neural networks based on iterative one-hop message passing have been shown to struggle in harnessing information from distant nodes effectively. Conversely, graph transformers allow each node to attend to all other nodes directly, but suffer from high computational complexity and have to rely on ad-hoc positional encoding to bake in the graph inductive bias. In this paper, we propose a new architecture to reconcile these challenges. Our approach stems from the recent breakthroughs in long-range modeling provided by deep state-space models on sequential data: for a given target node, our model aggregates other nodes by their shortest distances to the target and uses a parallelizable linear recurrent network over the chain of distances to provide a natural encoding of its neighborhood structure. With no need for positional encoding, we empirically show that the performance of our model is highly competitive compared with that of state-of-the-art graph transformers on various benchmarks, at a drastically reduced computational complexity. In addition, we show that our model is theoretically more expressive than one-hop message passing neural networks.

Simplifying Transformer Blocks

A simple design recipe for deep Transformers is to compose identical building blocks. But standard transformer blocks are far from simple, interweaving attention and MLP sub-blocks with skip connections & normalisation layers in precise arrangements. This complexity leads to brittle architectures, where seemingly minor changes can significantly reduce training speed, or render models untrainable. In this work, we ask to what extent the standard transformer block can be simplified? Combining signal propagation theory and empirical observations, we motivate modifications that allow many block components to be removed with no loss of training speed, including skip connections, projection or value parameters, sequential sub-blocks and normalisation layers. In experiments on both autoregressive decoder-only and BERT encoder-only models, our simplified transformers emulate the per-update training speed and performance of standard transformers, while enjoying 15% faster training throughput, and using 15% fewer parameters.

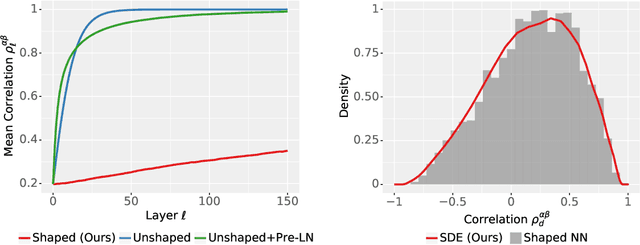
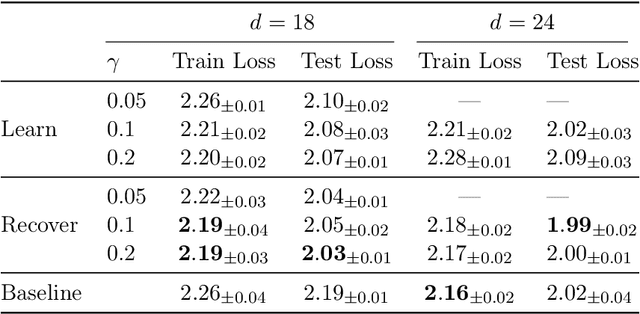
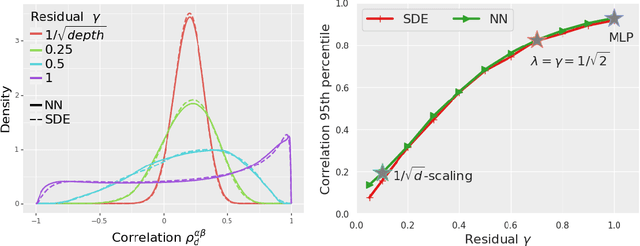
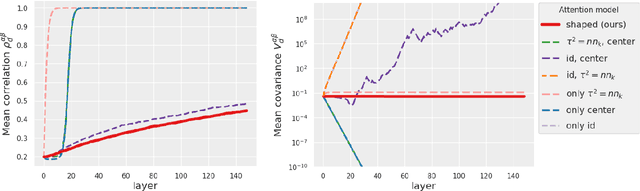
The Shaped Transformer: Attention Models in the Infinite Depth-and-Width Limit

In deep learning theory, the covariance matrix of the representations serves as a proxy to examine the network's trainability. Motivated by the success of Transformers, we study the covariance matrix of a modified Softmax-based attention model with skip connections in the proportional limit of infinite-depth-and-width. We show that at initialization the limiting distribution can be described by a stochastic differential equation (SDE) indexed by the depth-to-width ratio. To achieve a well-defined stochastic limit, the Transformer's attention mechanism is modified by centering the Softmax output at identity, and scaling the Softmax logits by a width-dependent temperature parameter. We examine the stability of the network through the corresponding SDE, showing how the scale of both the drift and diffusion can be elegantly controlled with the aid of residual connections. The existence of a stable SDE implies that the covariance structure is well-behaved, even for very large depth and width, thus preventing the notorious issues of rank degeneracy in deep attention models. Finally, we show, through simulations, that the SDE provides a surprisingly good description of the corresponding finite-size model. We coin the name shaped Transformer for these architectural modifications.

Deep Transformers without Shortcuts: Modifying Self-attention for Faithful Signal Propagation

Skip connections and normalisation layers form two standard architectural components that are ubiquitous for the training of Deep Neural Networks (DNNs), but whose precise roles are poorly understood. Recent approaches such as Deep Kernel Shaping have made progress towards reducing our reliance on them, using insights from wide NN kernel theory to improve signal propagation in vanilla DNNs (which we define as networks without skips or normalisation). However, these approaches are incompatible with the self-attention layers present in transformers, whose kernels are intrinsically more complicated to analyse and control. And so the question remains: is it possible to train deep vanilla transformers? We answer this question in the affirmative by designing several approaches that use combinations of parameter initialisations, bias matrices and location-dependent rescaling to achieve faithful signal propagation in vanilla transformers. Our methods address various intricacies specific to signal propagation in transformers, including the interaction with positional encoding and causal masking. In experiments on WikiText-103 and C4, our approaches enable deep transformers without normalisation to train at speeds matching their standard counterparts, and deep vanilla transformers to reach the same performance as standard ones after about 5 times more iterations.

UncertaINR: Uncertainty Quantification of End-to-End Implicit Neural Representations for Computed Tomography

Implicit neural representations (INRs) have achieved impressive results for scene reconstruction and computer graphics, where their performance has primarily been assessed on reconstruction accuracy. However, in medical imaging, where the reconstruction problem is underdetermined and model predictions inform high-stakes diagnoses, uncertainty quantification of INR inference is critical. To that end, we study UncertaINR: a Bayesian reformulation of INR-based image reconstruction, for computed tomography (CT). We test several Bayesian deep learning implementations of UncertaINR and find that they achieve well-calibrated uncertainty, while retaining accuracy competitive with other classical, INR-based, and CNN-based reconstruction techniques. In contrast to the best-performing prior approaches, UncertaINR does not require a large training dataset, but only a handful of validation images.

Probabilistic fine-tuning of pruning masks and PAC-Bayes self-bounded learning

We study an approach to learning pruning masks by optimizing the expected loss of stochastic pruning masks, i.e., masks which zero out each weight independently with some weight-specific probability. We analyze the training dynamics of the induced stochastic predictor in the setting of linear regression, and observe a data-adaptive L1 regularization term, in contrast to the dataadaptive L2 regularization term known to underlie dropout in linear regression. We also observe a preference to prune weights that are less well-aligned with the data labels. We evaluate probabilistic fine-tuning for optimizing stochastic pruning masks for neural networks, starting from masks produced by several baselines. In each case, we see improvements in test error over baselines, even after we threshold fine-tuned stochastic pruning masks. Finally, since a stochastic pruning mask induces a stochastic neural network, we consider training the weights and/or pruning probabilities simultaneously to minimize a PAC-Bayes bound on generalization error. Using data-dependent priors, we obtain a selfbounded learning algorithm with strong performance and numerically tight bounds. In the linear model, we show that a PAC-Bayes generalization error bound is controlled by the magnitude of the change in feature alignment between the 'prior' and 'posterior' data.

Stable ResNet

Deep ResNet architectures have achieved state of the art performance on many tasks. While they solve the problem of gradient vanishing, they might suffer from gradient exploding as the depth becomes large (Yang et al. 2017). Moreover, recent results have shown that ResNet might lose expressivity as the depth goes to infinity (Yang et al. 2017, Hayou et al. 2019). To resolve these issues, we introduce a new class of ResNet architectures, called Stable ResNet, that have the property of stabilizing the gradient while ensuring expressivity in the infinite depth limit.

Bayesian Deep Ensembles via the Neural Tangent Kernel

We explore the link between deep ensembles and Gaussian processes (GPs) through the lens of the Neural Tangent Kernel (NTK): a recent development in understanding the training dynamics of wide neural networks (NNs). Previous work has shown that even in the infinite width limit, when NNs become GPs, there is no GP posterior interpretation to a deep ensemble trained with squared error loss. We introduce a simple modification to standard deep ensembles training, through addition of a computationally-tractable, randomised and untrainable function to each ensemble member, that enables a posterior interpretation in the infinite width limit. When ensembled together, our trained NNs give an approximation to a posterior predictive distribution, and we prove that our Bayesian deep ensembles make more conservative predictions than standard deep ensembles in the infinite width limit. Finally, using finite width NNs we demonstrate that our Bayesian deep ensembles faithfully emulate the analytic posterior predictive when available, and can outperform standard deep ensembles in various out-of-distribution settings, for both regression and classification tasks.