Understanding and Minimising Outlier Features in Neural Network Training

Outlier Features (OF) are neurons whose activation magnitudes significantly exceed the average over a neural network's (NN) width. They are well known to emerge during standard transformer training and have the undesirable effect of hindering quantisation in afflicted models. Despite their practical importance, little is known behind why OFs emerge during training, nor how one can minimise them. Our work focuses on the above questions, first identifying several quantitative metrics, such as the kurtosis over neuron activation norms, to measure OFs. With these metrics, we study how architectural and optimisation choices influence OFs, and provide practical insights to minimise OFs during training. As highlights, we emphasise the importance of controlling signal propagation throughout training, and propose the Outlier Protected transformer block, which removes standard Pre-Norm layers to mitigate OFs, without loss of convergence speed or training stability. Overall, our findings shed new light on our understanding of, our ability to prevent, and the complexity of this important facet in NN training dynamics.

Why do Learning Rates Transfer? Reconciling Optimization and Scaling Limits for Deep Learning

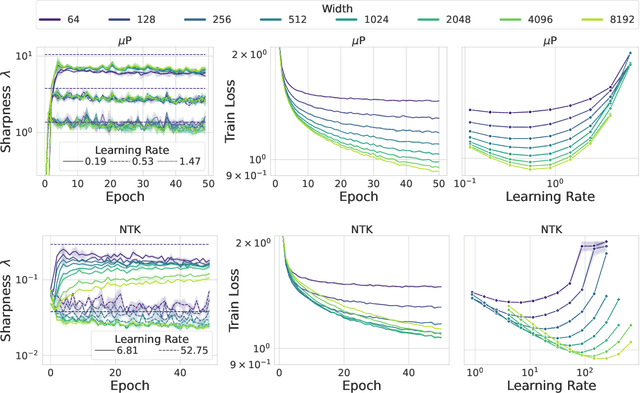
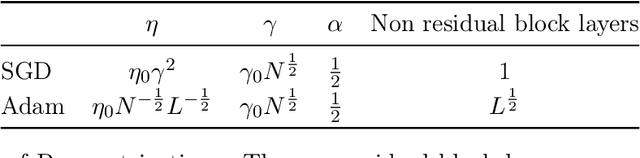
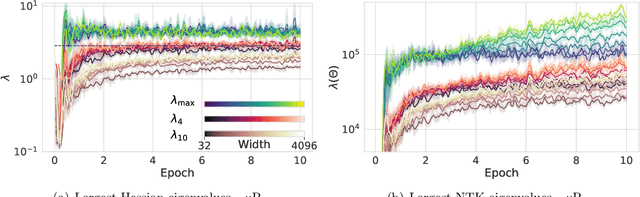
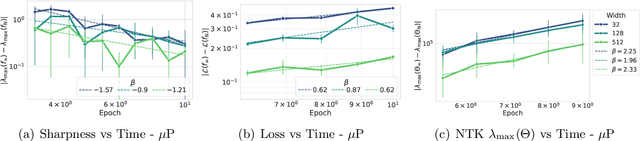
Recently, there has been growing evidence that if the width and depth of a neural network are scaled toward the so-called rich feature learning limit ($\mu$P and its depth extension), then some hyperparameters - such as the learning rate - exhibit transfer from small to very large models, thus reducing the cost of hyperparameter tuning. From an optimization perspective, this phenomenon is puzzling, as it implies that the loss landscape is remarkably consistent across very different model sizes. In this work, we find empirical evidence that learning rate transfer can be attributed to the fact that under $\mu$P and its depth extension, the largest eigenvalue of the training loss Hessian (i.e. the sharpness) is largely independent of the width and depth of the network for a sustained period of training time. On the other hand, we show that under the neural tangent kernel (NTK) regime, the sharpness exhibits very different dynamics at different scales, thus preventing learning rate transfer. But what causes these differences in the sharpness dynamics? Through a connection between the spectra of the Hessian and the NTK matrix, we argue that the cause lies in the presence (for $\mu$P) or progressive absence (for the NTK regime) of feature learning, which results in a different evolution of the NTK, and thus of the sharpness. We corroborate our claims with a substantial suite of experiments, covering a wide range of datasets and architectures: from ResNets and Vision Transformers trained on benchmark vision datasets to Transformers-based language models trained on WikiText

How Good is a Single Basin?

The multi-modal nature of neural loss landscapes is often considered to be the main driver behind the empirical success of deep ensembles. In this work, we probe this belief by constructing various "connected" ensembles which are restricted to lie in the same basin. Through our experiments, we demonstrate that increased connectivity indeed negatively impacts performance. However, when incorporating the knowledge from other basins implicitly through distillation, we show that the gap in performance can be mitigated by re-discovering (multi-basin) deep ensembles within a single basin. Thus, we conjecture that while the extra-basin knowledge is at least partially present in any given basin, it cannot be easily harnessed without learning it from other basins.

Disentangling Linear Mode-Connectivity

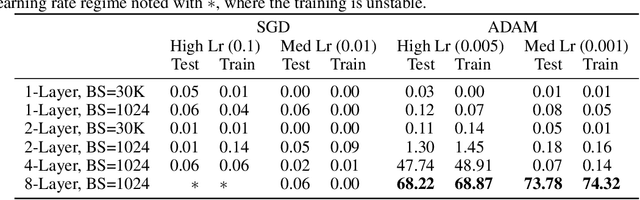
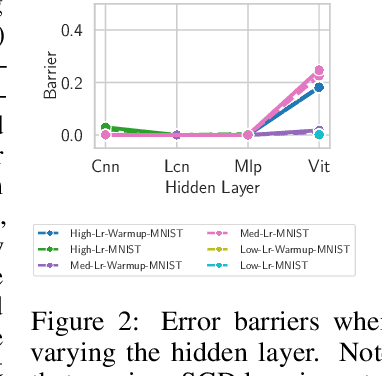
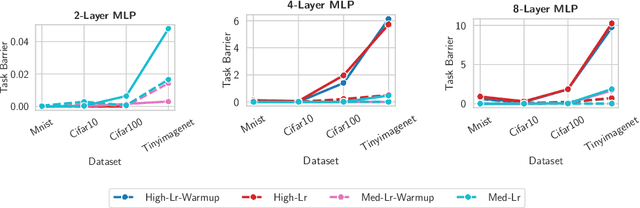
Linear mode-connectivity (LMC) (or lack thereof) is one of the intriguing characteristics of neural network loss landscapes. While empirically well established, it unfortunately still lacks a proper theoretical understanding. Even worse, although empirical data points are abound, a systematic study of when networks exhibit LMC is largely missing in the literature. In this work we aim to close this gap. We explore how LMC is affected by three factors: (1) architecture (sparsity, weight-sharing), (2) training strategy (optimization setup) as well as (3) the underlying dataset. We place particular emphasis on minimal but non-trivial settings, removing as much unnecessary complexity as possible. We believe that our insights can guide future theoretical works on uncovering the inner workings of LMC.

Depthwise Hyperparameter Transfer in Residual Networks: Dynamics and Scaling Limit

The cost of hyperparameter tuning in deep learning has been rising with model sizes, prompting practitioners to find new tuning methods using a proxy of smaller networks. One such proposal uses $\mu$P parameterized networks, where the optimal hyperparameters for small width networks transfer to networks with arbitrarily large width. However, in this scheme, hyperparameters do not transfer across depths. As a remedy, we study residual networks with a residual branch scale of $1/\sqrt{\text{depth}}$ in combination with the $\mu$P parameterization. We provide experiments demonstrating that residual architectures including convolutional ResNets and Vision Transformers trained with this parameterization exhibit transfer of optimal hyperparameters across width and depth on CIFAR-10 and ImageNet. Furthermore, our empirical findings are supported and motivated by theory. Using recent developments in the dynamical mean field theory (DMFT) description of neural network learning dynamics, we show that this parameterization of ResNets admits a well-defined feature learning joint infinite-width and infinite-depth limit and show convergence of finite-size network dynamics towards this limit.

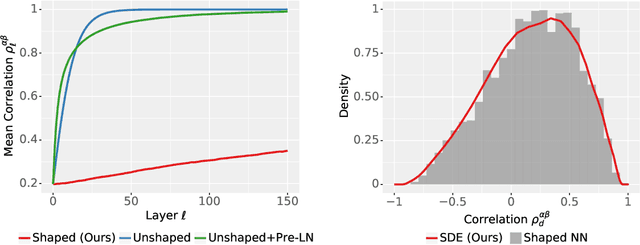
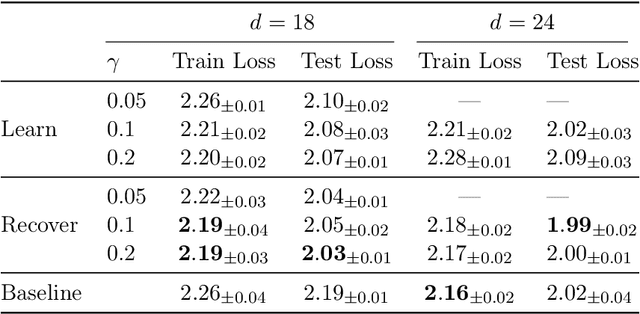
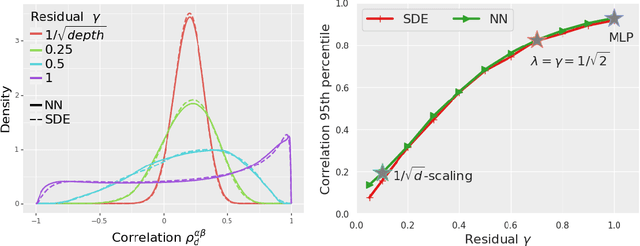
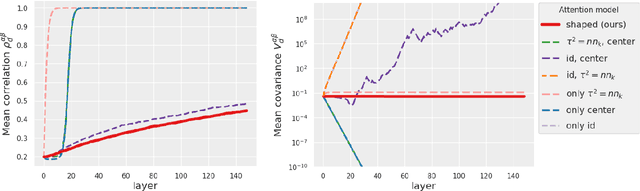
The Shaped Transformer: Attention Models in the Infinite Depth-and-Width Limit

In deep learning theory, the covariance matrix of the representations serves as a proxy to examine the network's trainability. Motivated by the success of Transformers, we study the covariance matrix of a modified Softmax-based attention model with skip connections in the proportional limit of infinite-depth-and-width. We show that at initialization the limiting distribution can be described by a stochastic differential equation (SDE) indexed by the depth-to-width ratio. To achieve a well-defined stochastic limit, the Transformer's attention mechanism is modified by centering the Softmax output at identity, and scaling the Softmax logits by a width-dependent temperature parameter. We examine the stability of the network through the corresponding SDE, showing how the scale of both the drift and diffusion can be elegantly controlled with the aid of residual connections. The existence of a stable SDE implies that the covariance structure is well-behaved, even for very large depth and width, thus preventing the notorious issues of rank degeneracy in deep attention models. Finally, we show, through simulations, that the SDE provides a surprisingly good description of the corresponding finite-size model. We coin the name shaped Transformer for these architectural modifications.

Dynamic Context Pruning for Efficient and Interpretable Autoregressive Transformers

Autoregressive Transformers adopted in Large Language Models (LLMs) are hard to scale to long sequences. Despite several works trying to reduce their computational cost, most of LLMs still adopt attention layers between all pairs of tokens in the sequence, thus incurring a quadratic cost. In this study, we present a novel approach that dynamically prunes contextual information while preserving the model's expressiveness, resulting in reduced memory and computational requirements during inference. Our method employs a learnable mechanism that determines which uninformative tokens can be dropped from the context at any point across the generation process. By doing so, our approach not only addresses performance concerns but also enhances interpretability, providing valuable insight into the model's decision-making process. Our technique can be applied to existing pre-trained models through a straightforward fine-tuning process, and the pruning strength can be specified by a sparsity parameter. Notably, our empirical findings demonstrate that we can effectively prune up to 80\% of the context without significant performance degradation on downstream tasks, offering a valuable tool for mitigating inference costs. Our reference implementation achieves up to $2\times$ increase in inference throughput and even greater memory savings.

Achieving a Better Stability-Plasticity Trade-off via Auxiliary Networks in Continual Learning

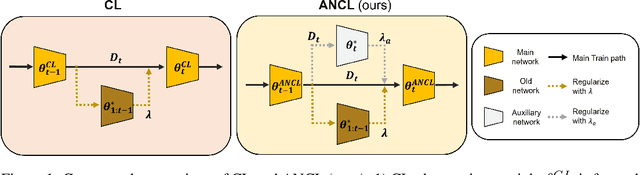
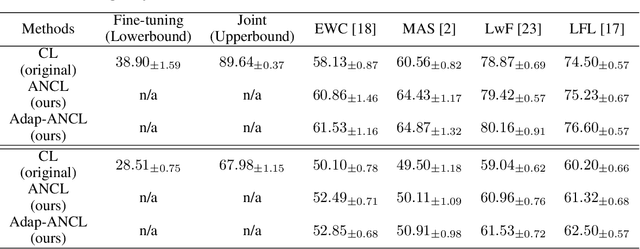
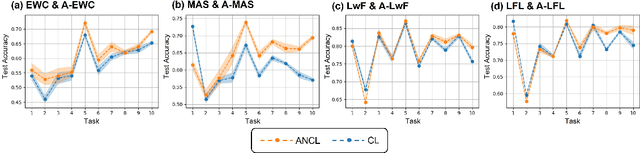
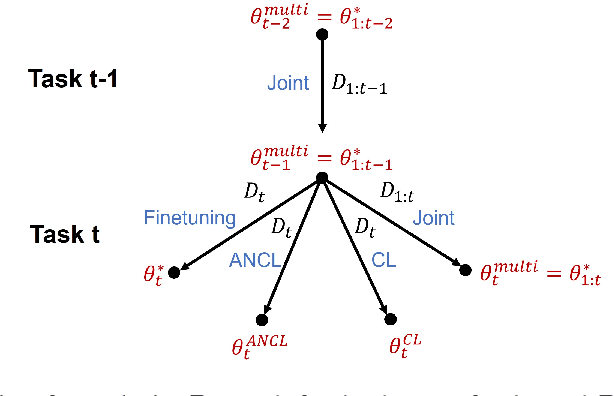
In contrast to the natural capabilities of humans to learn new tasks in a sequential fashion, neural networks are known to suffer from catastrophic forgetting, where the model's performances on old tasks drop dramatically after being optimized for a new task. Since then, the continual learning (CL) community has proposed several solutions aiming to equip the neural network with the ability to learn the current task (plasticity) while still achieving high accuracy on the previous tasks (stability). Despite remarkable improvements, the plasticity-stability trade-off is still far from being solved and its underlying mechanism is poorly understood. In this work, we propose Auxiliary Network Continual Learning (ANCL), a novel method that applies an additional auxiliary network which promotes plasticity to the continually learned model which mainly focuses on stability. More concretely, the proposed framework materializes in a regularizer that naturally interpolates between plasticity and stability, surpassing strong baselines on task incremental and class incremental scenarios. Through extensive analyses on ANCL solutions, we identify some essential principles beneath the stability-plasticity trade-off.

The Curious Case of Benign Memorization

Despite the empirical advances of deep learning across a variety of learning tasks, our theoretical understanding of its success is still very restricted. One of the key challenges is the overparametrized nature of modern models, enabling complete overfitting of the data even if the labels are randomized, i.e. networks can completely memorize all given patterns. While such a memorization capacity seems worrisome, in this work we show that under training protocols that include data augmentation, neural networks learn to memorize entirely random labels in a benign way, i.e. they learn embeddings that lead to highly non-trivial performance under nearest neighbour probing. We demonstrate that deep models have the surprising ability to separate noise from signal by distributing the task of memorization and feature learning to different layers. As a result, only the very last layers are used for memorization, while preceding layers encode performant features which remain largely unaffected by the label noise. We explore the intricate role of the augmentations used for training and identify a memorization-generalization trade-off in terms of their diversity, marking a clear distinction to all previous works. Finally, we give a first explanation for the emergence of benign memorization by showing that malign memorization under data augmentation is infeasible due to the insufficient capacity of the model for the increased sample size. As a consequence, the network is forced to leverage the correlated nature of the augmentations and as a result learns meaningful features. To complete the picture, a better theory of feature learning in deep neural networks is required to fully understand the origins of this phenomenon.

Signal Propagation in Transformers: Theoretical Perspectives and the Role of Rank Collapse

Transformers have achieved remarkable success in several domains, ranging from natural language processing to computer vision. Nevertheless, it has been recently shown that stacking self-attention layers - the distinctive architectural component of Transformers - can result in rank collapse of the tokens' representations at initialization. The question of if and how rank collapse affects training is still largely unanswered, and its investigation is necessary for a more comprehensive understanding of this architecture. In this work, we shed new light on the causes and the effects of this phenomenon. First, we show that rank collapse of the tokens' representations hinders training by causing the gradients of the queries and keys to vanish at initialization. Furthermore, we provide a thorough description of the origin of rank collapse and discuss how to prevent it via an appropriate depth-dependent scaling of the residual branches. Finally, our analysis unveils that specific architectural hyperparameters affect the gradients of queries and values differently, leading to disproportionate gradient norms. This suggests an explanation for the widespread use of adaptive methods for Transformers' optimization.