Fast and Geometrically Grounded Lorentz Neural Networks

Hyperbolic space is quickly gaining traction as a promising geometry for hierarchical and robust representation learning. A core open challenge is the development of a mathematical formulation of hyperbolic neural networks that is both efficient and captures the key properties of hyperbolic space. The Lorentz model of hyperbolic space has been shown to enable both fast forward and backward propagation. However, we prove that, with the current formulation of Lorentz linear layers, the hyperbolic norms of the outputs scale logarithmically with the number of gradient descent steps, nullifying the key advantage of hyperbolic geometry. We propose a new Lorentz linear layer grounded in the well-known ``distance-to-hyperplane" formulation. We prove that our formulation results in the usual linear scaling of output hyperbolic norms with respect to the number of gradient descent steps. Our new formulation, together with further algorithmic efficiencies through Lorentzian activation functions and a new caching strategy results in neural networks fully abiding by hyperbolic geometry while simultaneously bridging the computation gap to Euclidean neural networks. Code available at: https://github.com/robertdvdk/hyperbolic-fully-connected.

Scalable Non-Equivariant 3D Molecule Generation via Rotational Alignment

Equivariant diffusion models have achieved impressive performance in 3D molecule generation. These models incorporate Euclidean symmetries of 3D molecules by utilizing an SE(3)-equivariant denoising network. However, specialized equivariant architectures limit the scalability and efficiency of diffusion models. In this paper, we propose an approach that relaxes such equivariance constraints. Specifically, our approach learns a sample-dependent SO(3) transformation for each molecule to construct an aligned latent space. A non-equivariant diffusion model is then trained over the aligned representations. Experimental results demonstrate that our approach performs significantly better than previously reported non-equivariant models. It yields sample quality comparable to state-of-the-art equivariant diffusion models and offers improved training and sampling efficiency. Our code is available at https://github.com/skeletondyh/RADM

Generalized Interpolating Discrete Diffusion

While state-of-the-art language models achieve impressive results through next-token prediction, they have inherent limitations such as the inability to revise already generated tokens. This has prompted exploration of alternative approaches such as discrete diffusion. However, masked diffusion, which has emerged as a popular choice due to its simplicity and effectiveness, reintroduces this inability to revise words. To overcome this, we generalize masked diffusion and derive the theoretical backbone of a family of general interpolating discrete diffusion (GIDD) processes offering greater flexibility in the design of the noising processes. Leveraging a novel diffusion ELBO, we achieve compute-matched state-of-the-art performance in diffusion language modeling. Exploiting GIDD's flexibility, we explore a hybrid approach combining masking and uniform noise, leading to improved sample quality and unlocking the ability for the model to correct its own mistakes, an area where autoregressive models notoriously have struggled. Our code and models are open-source: https://github.com/dvruette/gidd/

Recurrent Distance-Encoding Neural Networks for Graph Representation Learning

Graph neural networks based on iterative one-hop message passing have been shown to struggle in harnessing information from distant nodes effectively. Conversely, graph transformers allow each node to attend to all other nodes directly, but suffer from high computational complexity and have to rely on ad-hoc positional encoding to bake in the graph inductive bias. In this paper, we propose a new architecture to reconcile these challenges. Our approach stems from the recent breakthroughs in long-range modeling provided by deep state-space models on sequential data: for a given target node, our model aggregates other nodes by their shortest distances to the target and uses a parallelizable linear recurrent network over the chain of distances to provide a natural encoding of its neighborhood structure. With no need for positional encoding, we empirically show that the performance of our model is highly competitive compared with that of state-of-the-art graph transformers on various benchmarks, at a drastically reduced computational complexity. In addition, we show that our model is theoretically more expressive than one-hop message passing neural networks.

Propagation Model Search for Graph Neural Networks

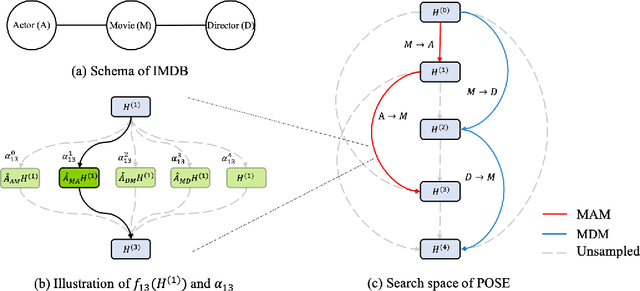
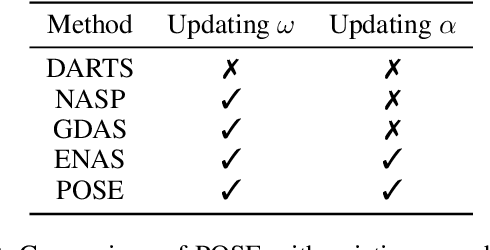
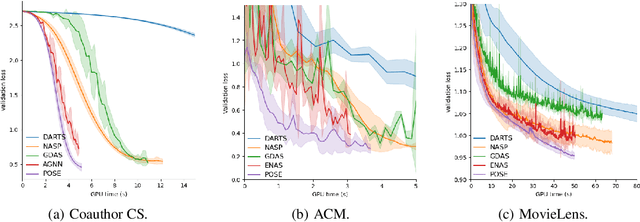
This paper presents a novel neural architecture search (NAS) framework for graph neural networks (GNNs). We design an expressive search space that focuses on a common and critical component of GNNs -- propagation model. Specifically, we search for propagation matrices and the connections between propagation steps. Our search space covers various graph types, e.g., homogeneous graphs, heterogeneous graphs, and can be naturally extended to higher-dimensional recommender systems and spatial-temporal data. We propose a sampling-based one-shot NAS algorithm to search for appropriate propagation patterns efficiently. Extensive experiments in three different scenarios are used to evaluate the proposed framework. We show that the performance of the models obtained by our framework is better than state-of-the-art GNN methods. Furthermore, our framework can discover explainable meta-graphs in heterogeneous graphs.

Learning to Identify High Betweenness Centrality Nodes from Scratch: A Novel Graph Neural Network Approach

Betweenness centrality (BC) is one of the most used centrality measures for network analysis, which seeks to describe the importance of nodes in a network in terms of the fraction of shortest paths that pass through them. It is key to many valuable applications, including community detection and network dismantling. Computing BC scores on large networks is computationally challenging due to high time complexity. Many approximation algorithms have been proposed to speed up the estimation of BC, which are mainly sampling-based. However, these methods are still prone to considerable execution time on large-scale networks, and their results are often exacerbated when small changes happen to the network structures. In this paper, we focus on identifying nodes with high BC in a graph, since many application scenarios are built upon retrieving nodes with top-k BC. Different from previous heuristic methods, we turn this task into a learning problem and design an encoder-decoder based framework to resolve the problem. More specifcally, the encoder leverages the network structure to encode each node into an embedding vector, which captures the important structural information of the node. The decoder transforms the embedding vector for each node into a scalar, which captures the relative rank of this node in terms of BC. We use the pairwise ranking loss to train the model to identify the orders of nodes regarding their BC. By training on small-scale networks, the learned model is capable of assigning relative BC scores to nodes for any unseen networks, and thus identifying the highly-ranked nodes. Comprehensive experiments on both synthetic and real-world networks demonstrate that, compared to representative baselines, our model drastically speeds up the prediction without noticeable sacrifce in accuracy, and outperforms the state-of-the-art by accuracy on several large real-world networks.