Ashwini Pokle
Learn to Guide Your Diffusion Model
Oct 01, 2025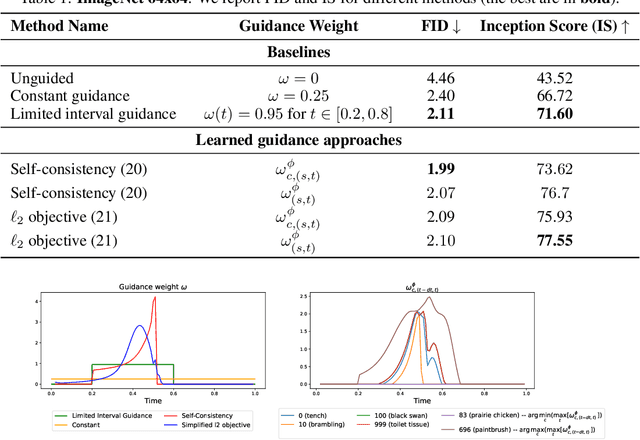
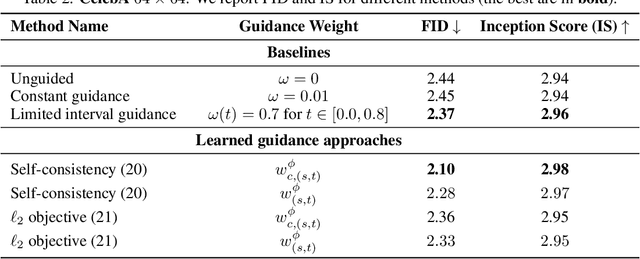
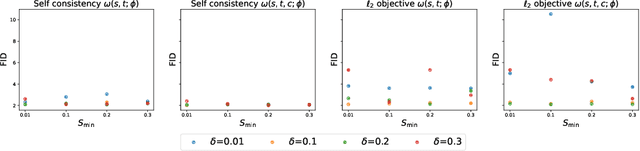

Abstract:Classifier-free guidance (CFG) is a widely used technique for improving the perceptual quality of samples from conditional diffusion models. It operates by linearly combining conditional and unconditional score estimates using a guidance weight $\omega$. While a large, static weight can markedly improve visual results, this often comes at the cost of poorer distributional alignment. In order to better approximate the target conditional distribution, we instead learn guidance weights $\omega_{c,(s,t)}$, which are continuous functions of the conditioning $c$, the time $t$ from which we denoise, and the time $s$ towards which we denoise. We achieve this by minimizing the distributional mismatch between noised samples from the true conditional distribution and samples from the guided diffusion process. We extend our framework to reward guided sampling, enabling the model to target distributions tilted by a reward function $R(x_0,c)$, defined on clean data and a conditioning $c$. We demonstrate the effectiveness of our methodology on low-dimensional toy examples and high-dimensional image settings, where we observe improvements in Fr\'echet inception distance (FID) for image generation. In text-to-image applications, we observe that employing a reward function given by the CLIP score leads to guidance weights that improve image-prompt alignment.
Consistency Models Made Easy
Jun 20, 2024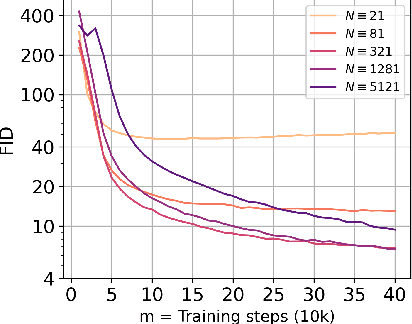
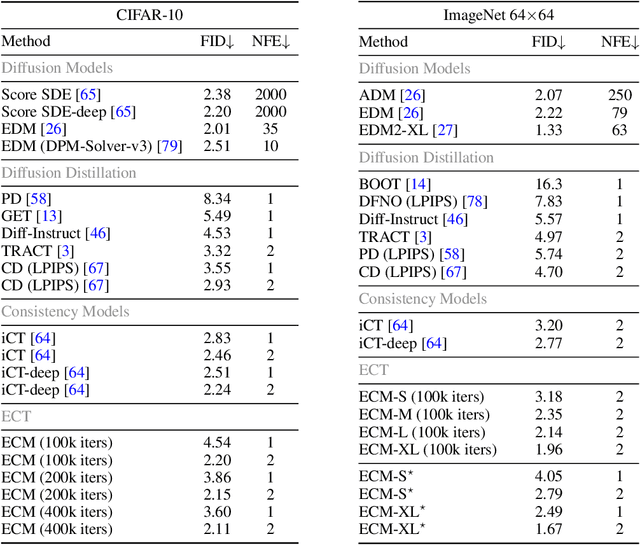
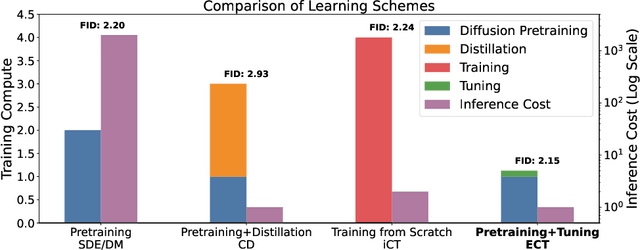

Abstract:Consistency models (CMs) are an emerging class of generative models that offer faster sampling than traditional diffusion models. CMs enforce that all points along a sampling trajectory are mapped to the same initial point. But this target leads to resource-intensive training: for example, as of 2024, training a SoTA CM on CIFAR-10 takes one week on 8 GPUs. In this work, we propose an alternative scheme for training CMs, vastly improving the efficiency of building such models. Specifically, by expressing CM trajectories via a particular differential equation, we argue that diffusion models can be viewed as a special case of CMs with a specific discretization. We can thus fine-tune a consistency model starting from a pre-trained diffusion model and progressively approximate the full consistency condition to stronger degrees over the training process. Our resulting method, which we term Easy Consistency Tuning (ECT), achieves vastly improved training times while indeed improving upon the quality of previous methods: for example, ECT achieves a 2-step FID of 2.73 on CIFAR10 within 1 hour on a single A100 GPU, matching Consistency Distillation trained of hundreds of GPU hours. Owing to this computational efficiency, we investigate the scaling law of CMs under ECT, showing that they seem to obey classic power law scaling, hinting at their ability to improve efficiency and performance at larger scales. Code (https://github.com/locuslab/ect) is available.
Deep Equilibrium Based Neural Operators for Steady-State PDEs
Nov 30, 2023



Abstract:Data-driven machine learning approaches are being increasingly used to solve partial differential equations (PDEs). They have shown particularly striking successes when training an operator, which takes as input a PDE in some family, and outputs its solution. However, the architectural design space, especially given structural knowledge of the PDE family of interest, is still poorly understood. We seek to remedy this gap by studying the benefits of weight-tied neural network architectures for steady-state PDEs. To achieve this, we first demonstrate that the solution of most steady-state PDEs can be expressed as a fixed point of a non-linear operator. Motivated by this observation, we propose FNO-DEQ, a deep equilibrium variant of the FNO architecture that directly solves for the solution of a steady-state PDE as the infinite-depth fixed point of an implicit operator layer using a black-box root solver and differentiates analytically through this fixed point resulting in $\mathcal{O}(1)$ training memory. Our experiments indicate that FNO-DEQ-based architectures outperform FNO-based baselines with $4\times$ the number of parameters in predicting the solution to steady-state PDEs such as Darcy Flow and steady-state incompressible Navier-Stokes. Finally, we show FNO-DEQ is more robust when trained with datasets with more noisy observations than the FNO-based baselines, demonstrating the benefits of using appropriate inductive biases in architectural design for different neural network based PDE solvers. Further, we show a universal approximation result that demonstrates that FNO-DEQ can approximate the solution to any steady-state PDE that can be written as a fixed point equation.
Path Independent Equilibrium Models Can Better Exploit Test-Time Computation
Nov 18, 2022



Abstract:Designing networks capable of attaining better performance with an increased inference budget is important to facilitate generalization to harder problem instances. Recent efforts have shown promising results in this direction by making use of depth-wise recurrent networks. We show that a broad class of architectures named equilibrium models display strong upwards generalization, and find that stronger performance on harder examples (which require more iterations of inference to get correct) strongly correlates with the path independence of the system -- its tendency to converge to the same steady-state behaviour regardless of initialization, given enough computation. Experimental interventions made to promote path independence result in improved generalization on harder problem instances, while those that penalize it degrade this ability. Path independence analyses are also useful on a per-example basis: for equilibrium models that have good in-distribution performance, path independence on out-of-distribution samples strongly correlates with accuracy. Our results help explain why equilibrium models are capable of strong upwards generalization and motivates future work that harnesses path independence as a general modelling principle to facilitate scalable test-time usage.
Deep Equilibrium Approaches to Diffusion Models
Oct 23, 2022



Abstract:Diffusion-based generative models are extremely effective in generating high-quality images, with generated samples often surpassing the quality of those produced by other models under several metrics. One distinguishing feature of these models, however, is that they typically require long sampling chains to produce high-fidelity images. This presents a challenge not only from the lenses of sampling time, but also from the inherent difficulty in backpropagating through these chains in order to accomplish tasks such as model inversion, i.e. approximately finding latent states that generate known images. In this paper, we look at diffusion models through a different perspective, that of a (deep) equilibrium (DEQ) fixed point model. Specifically, we extend the recent denoising diffusion implicit model (DDIM; Song et al. 2020), and model the entire sampling chain as a joint, multivariate fixed point system. This setup provides an elegant unification of diffusion and equilibrium models, and shows benefits in 1) single image sampling, as it replaces the fully-serial typical sampling process with a parallel one; and 2) model inversion, where we can leverage fast gradients in the DEQ setting to much more quickly find the noise that generates a given image. The approach is also orthogonal and thus complementary to other methods used to reduce the sampling time, or improve model inversion. We demonstrate our method's strong performance across several datasets, including CIFAR10, CelebA, and LSUN Bedrooms and Churches.
Contrasting the landscape of contrastive and non-contrastive learning
Mar 29, 2022
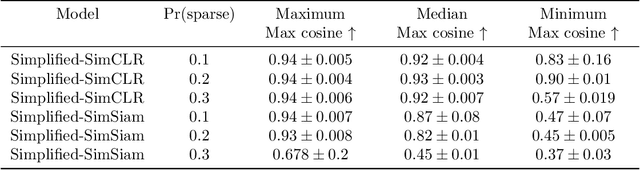

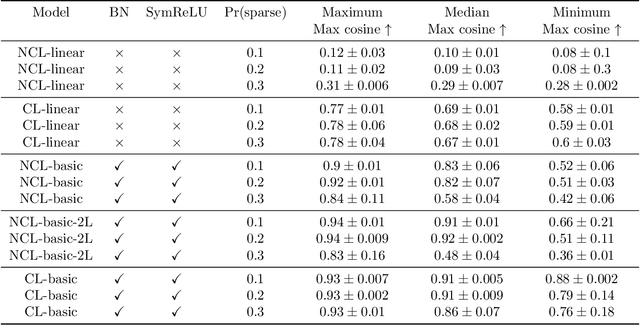
Abstract:A lot of recent advances in unsupervised feature learning are based on designing features which are invariant under semantic data augmentations. A common way to do this is contrastive learning, which uses positive and negative samples. Some recent works however have shown promising results for non-contrastive learning, which does not require negative samples. However, the non-contrastive losses have obvious "collapsed" minima, in which the encoders output a constant feature embedding, independent of the input. A folk conjecture is that so long as these collapsed solutions are avoided, the produced feature representations should be good. In our paper, we cast doubt on this story: we show through theoretical results and controlled experiments that even on simple data models, non-contrastive losses have a preponderance of non-collapsed bad minima. Moreover, we show that the training process does not avoid these minima.
Deep Local Trajectory Replanning and Control for Robot Navigation
May 13, 2019
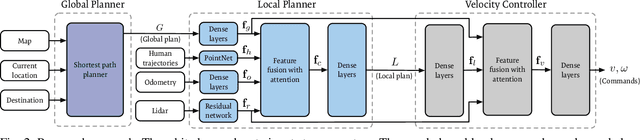
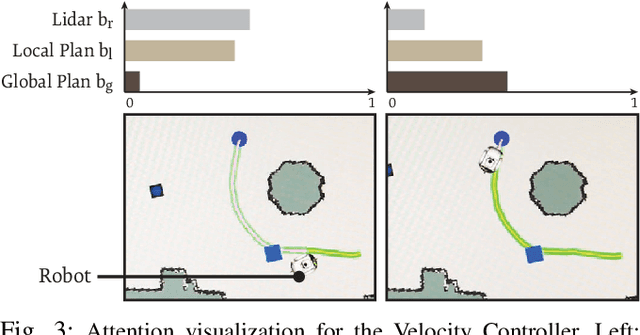
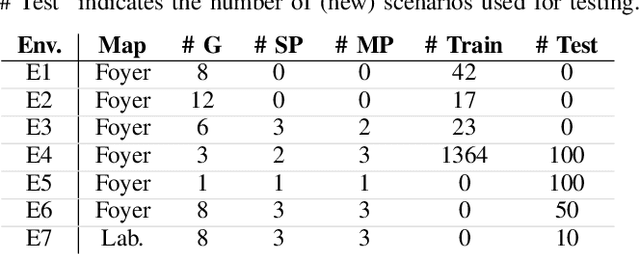
Abstract:We present a navigation system that combines ideas from hierarchical planning and machine learning. The system uses a traditional global planner to compute optimal paths towards a goal, and a deep local trajectory planner and velocity controller to compute motion commands. The latter components of the system adjust the behavior of the robot through attention mechanisms such that it moves towards the goal, avoids obstacles, and respects the space of nearby pedestrians. Both the structure of the proposed deep models and the use of attention mechanisms make the system's execution interpretable. Our simulation experiments suggest that the proposed architecture outperforms baselines that try to map global plan information and sensor data directly to velocity commands. In comparison to a hand-designed traditional navigation system, the proposed approach showed more consistent performance.
Translating Navigation Instructions in Natural Language to a High-Level Plan for Behavioral Robot Navigation
Sep 24, 2018



Abstract:We propose an end-to-end deep learning model for translating free-form natural language instructions to a high-level plan for behavioral robot navigation. We use attention models to connect information from both the user instructions and a topological representation of the environment. We evaluate our model's performance on a new dataset containing 10,050 pairs of navigation instructions. Our model significantly outperforms baseline approaches. Furthermore, our results suggest that it is possible to leverage the environment map as a relevant knowledge base to facilitate the translation of free-form navigational instruction.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge