Tanya Marwah
Walrus: A Cross-Domain Foundation Model for Continuum Dynamics
Nov 19, 2025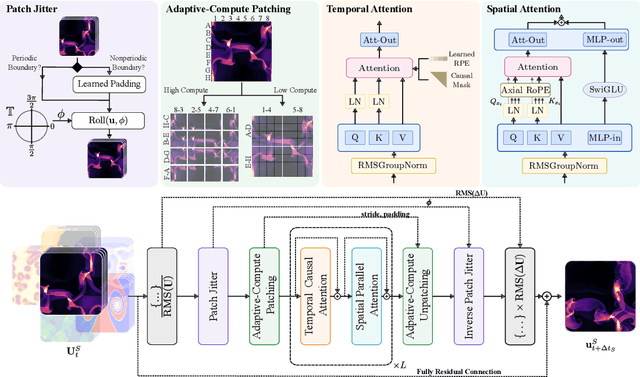


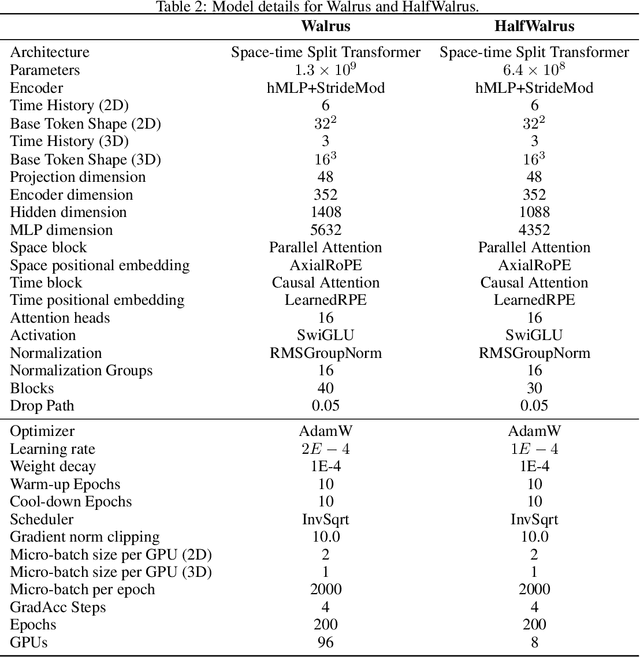
Abstract:Foundation models have transformed machine learning for language and vision, but achieving comparable impact in physical simulation remains a challenge. Data heterogeneity and unstable long-term dynamics inhibit learning from sufficiently diverse dynamics, while varying resolutions and dimensionalities challenge efficient training on modern hardware. Through empirical and theoretical analysis, we incorporate new approaches to mitigate these obstacles, including a harmonic-analysis-based stabilization method, load-balanced distributed 2D and 3D training strategies, and compute-adaptive tokenization. Using these tools, we develop Walrus, a transformer-based foundation model developed primarily for fluid-like continuum dynamics. Walrus is pretrained on nineteen diverse scenarios spanning astrophysics, geoscience, rheology, plasma physics, acoustics, and classical fluids. Experiments show that Walrus outperforms prior foundation models on both short and long term prediction horizons on downstream tasks and across the breadth of pretraining data, while ablation studies confirm the value of our contributions to forecast stability, training throughput, and transfer performance over conventional approaches. Code and weights are released for community use.
CodePDE: An Inference Framework for LLM-driven PDE Solver Generation
May 13, 2025Abstract:Partial differential equations (PDEs) are fundamental to modeling physical systems, yet solving them remains a complex challenge. Traditional numerical solvers rely on expert knowledge to implement and are computationally expensive, while neural-network-based solvers require large training datasets and often lack interpretability. In this work, we frame PDE solving as a code generation task and introduce CodePDE, the first inference framework for generating PDE solvers using large language models (LLMs). Leveraging advanced inference-time algorithms and scaling strategies, CodePDE unlocks critical capacities of LLM for PDE solving: reasoning, debugging, selfrefinement, and test-time scaling -- all without task-specific tuning. CodePDE achieves superhuman performance across a range of representative PDE problems. We also present a systematic empirical analysis of LLM generated solvers, analyzing their accuracy, efficiency, and numerical scheme choices. Our findings highlight the promise and the current limitations of LLMs in PDE solving, offering a new perspective on solver design and opportunities for future model development. Our code is available at https://github.com/LithiumDA/CodePDE.
Adapting Language Models via Token Translation
Nov 01, 2024Abstract:Modern large language models use a fixed tokenizer to effectively compress text drawn from a source domain. However, applying the same tokenizer to a new target domain often leads to inferior compression, more costly inference, and reduced semantic alignment. To address this deficiency, we introduce Sparse Sinkhorn Token Translation (S2T2). S2T2 trains a tailored tokenizer for the target domain and learns to translate between target and source tokens, enabling more effective reuse of the pre-trained next-source-token predictor. In our experiments with finetuned English language models, S2T2 improves both the perplexity and the compression of out-of-domain protein sequences, outperforming direct finetuning with either the source or target tokenizer. In addition, we find that token translations learned for smaller, less expensive models can be directly transferred to larger, more powerful models to reap the benefits of S2T2 at lower cost.
Towards characterizing the value of edge embeddings in Graph Neural Networks
Oct 13, 2024Abstract:Graph neural networks (GNNs) are the dominant approach to solving machine learning problems defined over graphs. Despite much theoretical and empirical work in recent years, our understanding of finer-grained aspects of architectural design for GNNs remains impoverished. In this paper, we consider the benefits of architectures that maintain and update edge embeddings. On the theoretical front, under a suitable computational abstraction for a layer in the model, as well as memory constraints on the embeddings, we show that there are natural tasks on graphical models for which architectures leveraging edge embeddings can be much shallower. Our techniques are inspired by results on time-space tradeoffs in theoretical computer science. Empirically, we show architectures that maintain edge embeddings almost always improve on their node-based counterparts -- frequently significantly so in topologies that have ``hub'' nodes.
On the Benefits of Memory for Modeling Time-Dependent PDEs
Sep 03, 2024Abstract:Data-driven techniques have emerged as a promising alternative to traditional numerical methods for solving partial differential equations (PDEs). These techniques frequently offer a better trade-off between computational cost and accuracy for many PDE families of interest. For time-dependent PDEs, existing methodologies typically treat PDEs as Markovian systems, i.e., the evolution of the system only depends on the ``current state'', and not the past states. However, distortion of the input signals -- e.g., due to discretization or low-pass filtering -- can render the evolution of the distorted signals non-Markovian. In this work, motivated by the Mori-Zwanzig theory of model reduction, we investigate the impact of architectures with memory for modeling PDEs: that is, when past states are explicitly used to predict the future. We introduce Memory Neural Operator (MemNO), a network based on the recent SSM architectures and Fourier Neural Operator (FNO). We empirically demonstrate on a variety of PDE families of interest that when the input is given on a low-resolution grid, MemNO significantly outperforms the baselines without memory, achieving more than 6 times less error on unseen PDEs. Via a combination of theory and experiments, we show that the effect of memory is particularly significant when the solution of the PDE has high frequency Fourier components (e.g., low-viscosity fluid dynamics), and it also increases robustness to observation noise.
UPS: Towards Foundation Models for PDE Solving via Cross-Modal Adaptation
Mar 11, 2024



Abstract:We introduce UPS (Unified PDE Solver), an effective and data-efficient approach to solve diverse spatiotemporal PDEs defined over various domains, dimensions, and resolutions. UPS unifies different PDEs into a consistent representation space and processes diverse collections of PDE data using a unified network architecture that combines LLMs with domain-specific neural operators. We train the network via a two-stage cross-modal adaptation process, leveraging ideas of modality alignment and multi-task learning. By adapting from pretrained LLMs and exploiting text-form meta information, we are able to use considerably fewer training samples than previous methods while obtaining strong empirical results. UPS outperforms existing baselines, often by a large margin, on a wide range of 1D and 2D datasets in PDEBench, achieving state-of-the-art results on 8 of 10 tasks considered. Meanwhile, it is capable of few-shot transfer to different PDE families, coefficients, and resolutions.
Deep Equilibrium Based Neural Operators for Steady-State PDEs
Nov 30, 2023



Abstract:Data-driven machine learning approaches are being increasingly used to solve partial differential equations (PDEs). They have shown particularly striking successes when training an operator, which takes as input a PDE in some family, and outputs its solution. However, the architectural design space, especially given structural knowledge of the PDE family of interest, is still poorly understood. We seek to remedy this gap by studying the benefits of weight-tied neural network architectures for steady-state PDEs. To achieve this, we first demonstrate that the solution of most steady-state PDEs can be expressed as a fixed point of a non-linear operator. Motivated by this observation, we propose FNO-DEQ, a deep equilibrium variant of the FNO architecture that directly solves for the solution of a steady-state PDE as the infinite-depth fixed point of an implicit operator layer using a black-box root solver and differentiates analytically through this fixed point resulting in $\mathcal{O}(1)$ training memory. Our experiments indicate that FNO-DEQ-based architectures outperform FNO-based baselines with $4\times$ the number of parameters in predicting the solution to steady-state PDEs such as Darcy Flow and steady-state incompressible Navier-Stokes. Finally, we show FNO-DEQ is more robust when trained with datasets with more noisy observations than the FNO-based baselines, demonstrating the benefits of using appropriate inductive biases in architectural design for different neural network based PDE solvers. Further, we show a universal approximation result that demonstrates that FNO-DEQ can approximate the solution to any steady-state PDE that can be written as a fixed point equation.
Disentangling the Mechanisms Behind Implicit Regularization in SGD
Nov 29, 2022



Abstract:A number of competing hypotheses have been proposed to explain why small-batch Stochastic Gradient Descent (SGD)leads to improved generalization over the full-batch regime, with recent work crediting the implicit regularization of various quantities throughout training. However, to date, empirical evidence assessing the explanatory power of these hypotheses is lacking. In this paper, we conduct an extensive empirical evaluation, focusing on the ability of various theorized mechanisms to close the small-to-large batch generalization gap. Additionally, we characterize how the quantities that SGD has been claimed to (implicitly) regularize change over the course of training. By using micro-batches, i.e. disjoint smaller subsets of each mini-batch, we empirically show that explicitly penalizing the gradient norm or the Fisher Information Matrix trace, averaged over micro-batches, in the large-batch regime recovers small-batch SGD generalization, whereas Jacobian-based regularizations fail to do so. This generalization performance is shown to often be correlated with how well the regularized model's gradient norms resemble those of small-batch SGD. We additionally show that this behavior breaks down as the micro-batch size approaches the batch size. Finally, we note that in this line of inquiry, positive experimental findings on CIFAR10 are often reversed on other datasets like CIFAR100, highlighting the need to test hypotheses on a wider collection of datasets.
Parametric Complexity Bounds for Approximating PDEs with Neural Networks
Mar 03, 2021Abstract:Recent empirical results show that deep networks can approximate solutions to high dimensional PDEs, seemingly escaping the curse of dimensionality. However many open questions remain regarding the theoretical basis for such approximations, including the number of parameters required. In this paper, we investigate the representational power of neural networks for approximating solutions to linear elliptic PDEs with Dirichlet Boundary conditions. We prove that when a PDE's coefficients are representable by small neural networks, the parameters required to approximate its solution scale polynomially with the input dimension $d$ and are proportional to the parameter counts of the coefficient neural networks. Our proof is based on constructing a neural network which simulates gradient descent in an appropriate Hilbert space which converges to the solution of the PDE. Moreover, we bound the size of the neural network needed to represent each iterate in terms of the neural network representing the previous iterate, resulting in a final network whose parameters depend polynomially on $d$ and does not depend on the volume of the domain.
Interactive Image Generation Using Scene Graphs
May 09, 2019

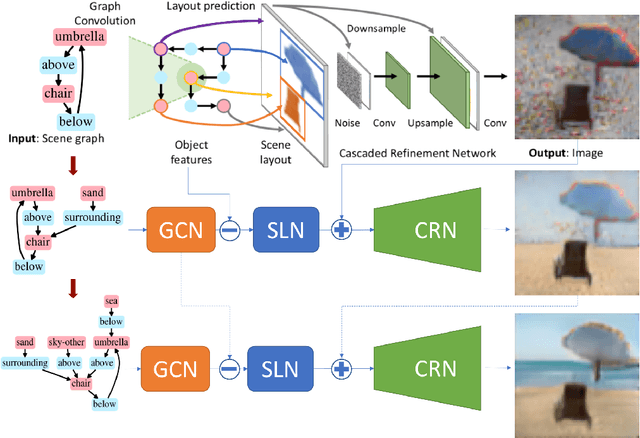

Abstract:Recent years have witnessed some exciting developments in the domain of generating images from scene-based text descriptions. These approaches have primarily focused on generating images from a static text description and are limited to generating images in a single pass. They are unable to generate an image interactively based on an incrementally additive text description (something that is more intuitive and similar to the way we describe an image). We propose a method to generate an image incrementally based on a sequence of graphs of scene descriptions (scene-graphs). We propose a recurrent network architecture that preserves the image content generated in previous steps and modifies the cumulative image as per the newly provided scene information. Our model utilizes Graph Convolutional Networks (GCN) to cater to variable-sized scene graphs along with Generative Adversarial image translation networks to generate realistic multi-object images without needing any intermediate supervision during training. We experiment with Coco-Stuff dataset which has multi-object images along with annotations describing the visual scene and show that our model significantly outperforms other approaches on the same dataset in generating visually consistent images for incrementally growing scene graphs.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge