Let's (not) just put things in Context: Test-Time Training for Long-Context LLMs

Progress on training and architecture strategies has enabled LLMs with millions of tokens in context length. However, empirical evidence suggests that such long-context LLMs can consume far more text than they can reliably use. On the other hand, it has been shown that inference-time compute can be used to scale performance of LLMs, often by generating thinking tokens, on challenging tasks involving multi-step reasoning. Through controlled experiments on sandbox long-context tasks, we find that such inference-time strategies show rapidly diminishing returns and fail at long context. We attribute these failures to score dilution, a phenomenon inherent to static self-attention. Further, we show that current inference-time strategies cannot retrieve relevant long-context signals under certain conditions. We propose a simple method that, through targeted gradient updates on the given context, provably overcomes limitations of static self-attention. We find that this shift in how inference-time compute is spent leads to consistently large performance improvements across models and long-context benchmarks. Our method leads to large 12.6 and 14.1 percentage point improvements for Qwen3-4B on average across subsets of LongBench-v2 and ZeroScrolls benchmarks. The takeaway is practical: for long context, a small amount of context-specific training is a better use of inference compute than current inference-time scaling strategies like producing more thinking tokens.

Let Me Think! A Long Chain-of-Thought Can Be Worth Exponentially Many Short Ones

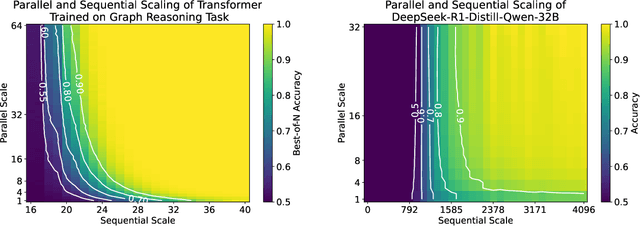
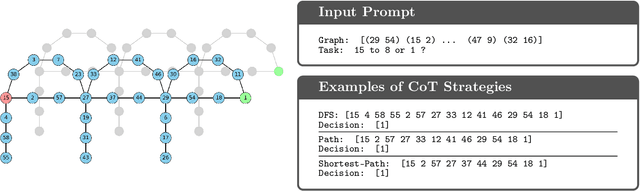
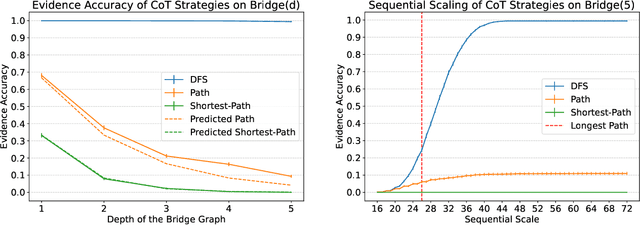
Inference-time computation has emerged as a promising scaling axis for improving large language model reasoning. However, despite yielding impressive performance, the optimal allocation of inference-time computation remains poorly understood. A central question is whether to prioritize sequential scaling (e.g., longer chains of thought) or parallel scaling (e.g., majority voting across multiple short chains of thought). In this work, we seek to illuminate the landscape of test-time scaling by demonstrating the existence of reasoning settings where sequential scaling offers an exponential advantage over parallel scaling. These settings are based on graph connectivity problems in challenging distributions of graphs. We validate our theoretical findings with comprehensive experiments across a range of language models, including models trained from scratch for graph connectivity with different chain of thought strategies as well as large reasoning models.

Echo Chamber: RL Post-training Amplifies Behaviors Learned in Pretraining

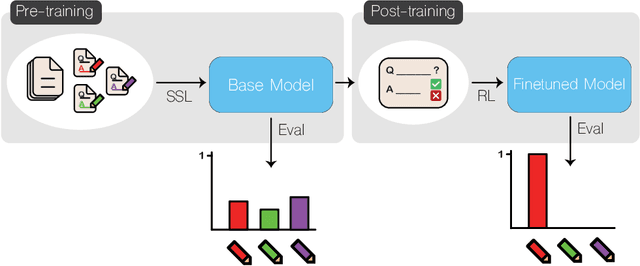
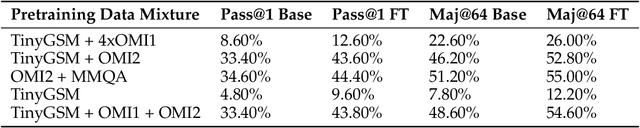
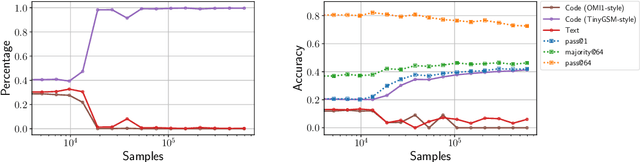
Reinforcement learning (RL)-based fine-tuning has become a crucial step in post-training language models for advanced mathematical reasoning and coding. Following the success of frontier reasoning models, recent work has demonstrated that RL fine-tuning consistently improves performance, even in smaller-scale models; however, the underlying mechanisms driving these improvements are not well-understood. Understanding the effects of RL fine-tuning requires disentangling its interaction with pretraining data composition, hyperparameters, and model scale, but such problems are exacerbated by the lack of transparency regarding the training data used in many existing models. In this work, we present a systematic end-to-end study of RL fine-tuning for mathematical reasoning by training models entirely from scratch on different mixtures of fully open datasets. We investigate the effects of various RL fine-tuning algorithms (PPO, GRPO, and Expert Iteration) across models of different scales. Our study reveals that RL algorithms consistently converge towards a dominant output distribution, amplifying patterns in the pretraining data. We also find that models of different scales trained on the same data mixture will converge to distinct output distributions, suggesting that there are scale-dependent biases in model generalization. Moreover, we find that RL post-training on simpler questions can lead to performance gains on harder ones, indicating that certain reasoning capabilities generalize across tasks. Our findings show that small-scale proxies in controlled settings can elicit interesting insights regarding the role of RL in shaping language model behavior.

To Backtrack or Not to Backtrack: When Sequential Search Limits Model Reasoning

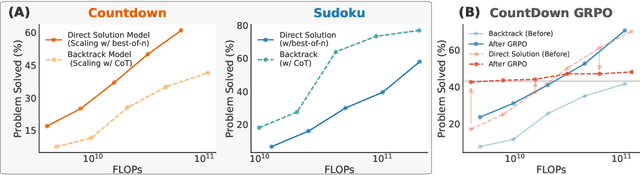
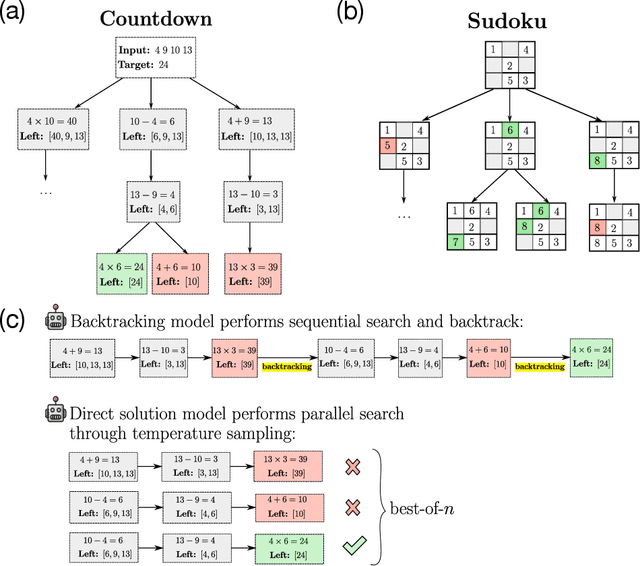
Recent advancements in large language models have significantly improved their reasoning abilities, particularly through techniques involving search and backtracking. Backtracking naturally scales test-time compute by enabling sequential, linearized exploration via long chain-of-thought (CoT) generation. However, this is not the only strategy for scaling test-time compute: parallel sampling with best-of-n selection provides an alternative that generates diverse solutions simultaneously. Despite the growing adoption of sequential search, its advantages over parallel sampling--especially under a fixed compute budget remain poorly understood. In this paper, we systematically compare these two approaches on two challenging reasoning tasks: CountDown and Sudoku. Surprisingly, we find that sequential search underperforms parallel sampling on CountDown but outperforms it on Sudoku, suggesting that backtracking is not universally beneficial. We identify two factors that can cause backtracking to degrade performance: (1) training on fixed search traces can lock models into suboptimal strategies, and (2) explicit CoT supervision can discourage "implicit" (non-verbalized) reasoning. Extending our analysis to reinforcement learning (RL), we show that models with backtracking capabilities benefit significantly from RL fine-tuning, while models without backtracking see limited, mixed gains. Together, these findings challenge the assumption that backtracking universally enhances LLM reasoning, instead revealing a complex interaction between task structure, training data, model scale, and learning paradigm.

The Role of Sparsity for Length Generalization in Transformers

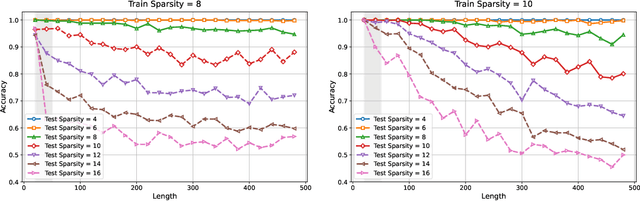
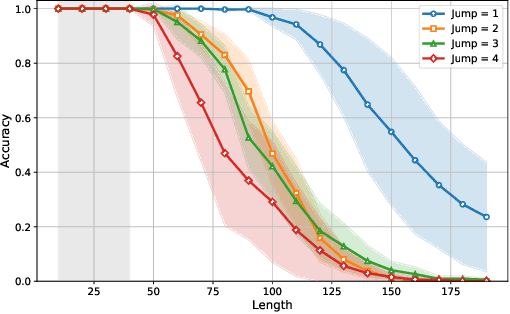
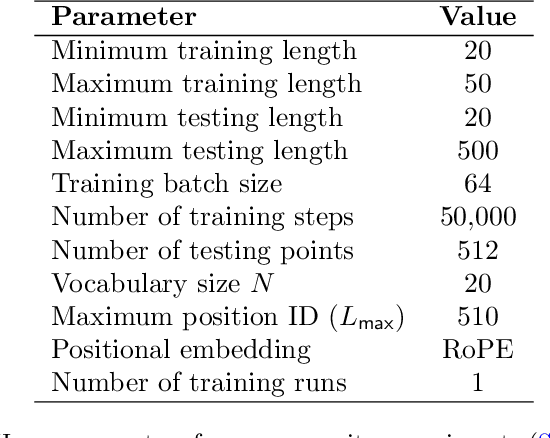
Training large language models to predict beyond their training context lengths has drawn much attention in recent years, yet the principles driving such behavior of length generalization remain underexplored. We propose a new theoretical framework to study length generalization for the next-token prediction task, as performed by decoder-only transformers. Conceptually, we show that length generalization occurs as long as each predicted token depends on a small (fixed) number of previous tokens. We formalize such tasks via a notion we call $k$-sparse planted correlation distributions, and show that an idealized model of transformers which generalize attention heads successfully length-generalize on such tasks. As a bonus, our theoretical model justifies certain techniques to modify positional embeddings which have been introduced to improve length generalization, such as position coupling. We support our theoretical results with experiments on synthetic tasks and natural language, which confirm that a key factor driving length generalization is a ``sparse'' dependency structure of each token on the previous ones. Inspired by our theory, we introduce Predictive Position Coupling, which trains the transformer to predict the position IDs used in a positional coupling approach. Predictive Position Coupling thereby allows us to broaden the array of tasks to which position coupling can successfully be applied to achieve length generalization.

Collective Model Intelligence Requires Compatible Specialization

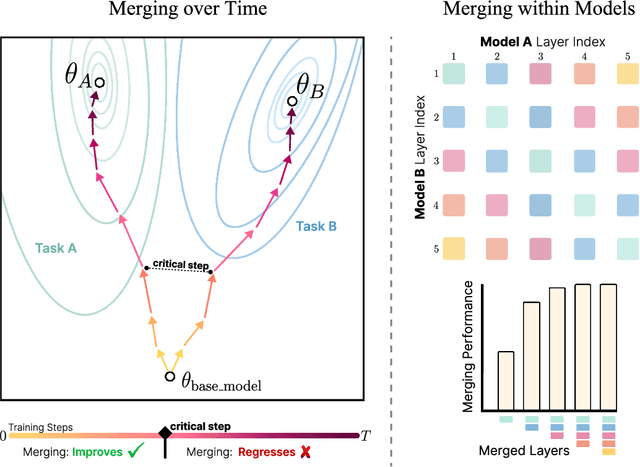
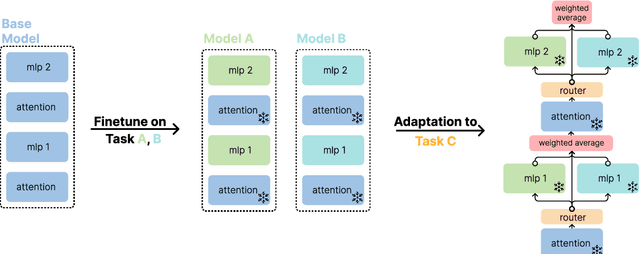
In this work, we explore the limitations of combining models by averaging intermediate features, referred to as model merging, and propose a new direction for achieving collective model intelligence through what we call compatible specialization. Current methods for model merging, such as parameter and feature averaging, struggle to effectively combine specialized models due to representational divergence during fine-tuning. As models specialize to their individual domains, their internal feature representations become increasingly incompatible, leading to poor performance when attempting to merge them for new tasks. We analyze this phenomenon using centered kernel alignment (CKA) and show that as models specialize, the similarity in their feature space structure diminishes, hindering their capacity for collective use. To address these challenges, we investigate routing-based merging strategies, which offer more flexible methods for combining specialized models by dynamically routing across different layers. This allows us to improve on existing methods by combining features from multiple layers rather than relying on fixed, layer-wise combinations. However, we find that these approaches still face limitations when layers within models are representationally incompatible. Our findings highlight the importance of designing new approaches for model merging that operate on well-defined input and output spaces, similar to how humans communicate through language rather than intermediate neural activations.

Mixture of Parrots: Experts improve memorization more than reasoning

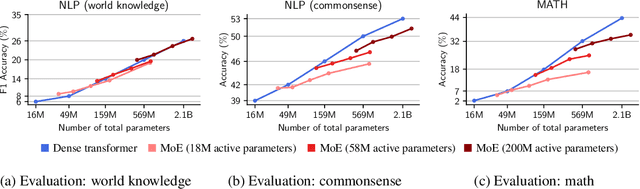
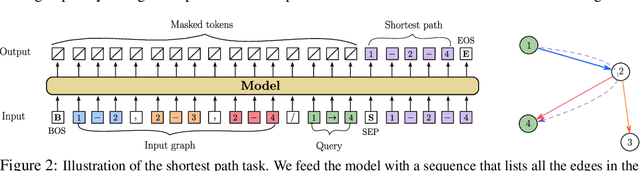
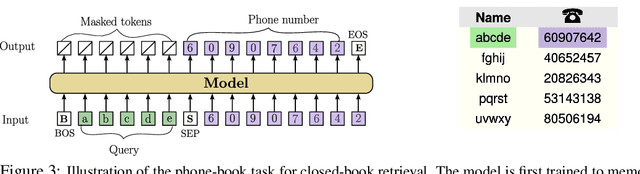
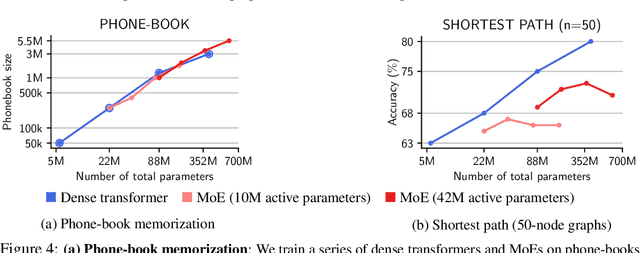
The Mixture-of-Experts (MoE) architecture enables a significant increase in the total number of model parameters with minimal computational overhead. However, it is not clear what performance tradeoffs, if any, exist between MoEs and standard dense transformers. In this paper, we show that as we increase the number of experts (while fixing the number of active parameters), the memorization performance consistently increases while the reasoning capabilities saturate. We begin by analyzing the theoretical limitations of MoEs at reasoning. We prove that there exist graph problems that cannot be solved by any number of experts of a certain width; however, the same task can be easily solved by a dense model with a slightly larger width. On the other hand, we find that on memory-intensive tasks, MoEs can effectively leverage a small number of active parameters with a large number of experts to memorize the data. We empirically validate these findings on synthetic graph problems and memory-intensive closed book retrieval tasks. Lastly, we pre-train a series of MoEs and dense transformers and evaluate them on commonly used benchmarks in math and natural language. We find that increasing the number of experts helps solve knowledge-intensive tasks, but fails to yield the same benefits for reasoning tasks.

LoRA Soups: Merging LoRAs for Practical Skill Composition Tasks

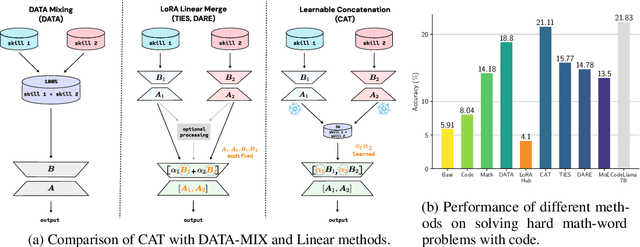
Low-Rank Adaptation (LoRA) is a popular technique for parameter-efficient fine-tuning of Large Language Models (LLMs). We study how different LoRA modules can be merged to achieve skill composition -- testing the performance of the merged model on a target task that involves combining multiple skills, each skill coming from a single LoRA. This setup is favorable when it is difficult to obtain training data for the target task and when it can be decomposed into multiple skills. First, we identify practically occurring use-cases that can be studied under the realm of skill composition, e.g. solving hard math-word problems with code, creating a bot to answer questions on proprietary manuals or about domain-specialized corpora. Our main contribution is to show that concatenation of LoRAs (CAT), which optimally averages LoRAs that were individually trained on different skills, outperforms existing model- and data- merging techniques; for instance on math-word problems, CAT beats these methods by an average of 43% and 12% respectively. Thus, this paper advocates model merging as an efficient way to solve compositional tasks and underscores CAT as a simple, compute-friendly and effective procedure. To our knowledge, this is the first work demonstrating the superiority of model merging over data mixing for binary skill composition tasks.

Universal Length Generalization with Turing Programs

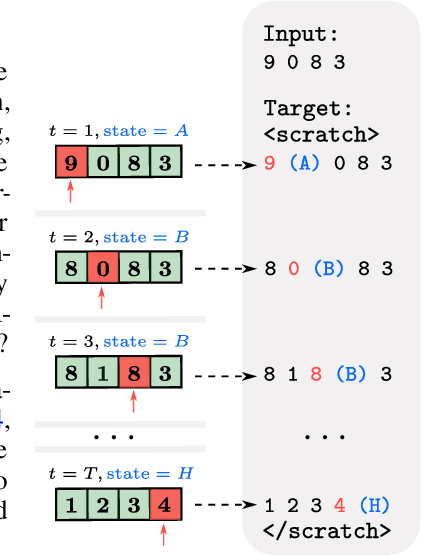
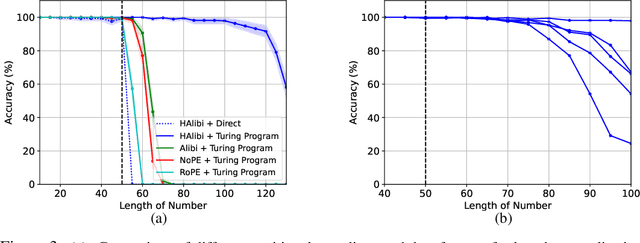
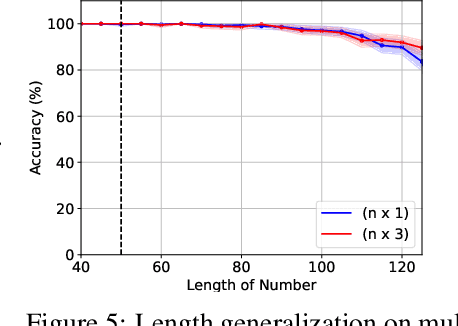
Length generalization refers to the ability to extrapolate from short training sequences to long test sequences and is a challenge for current large language models. While prior work has proposed some architecture or data format changes to achieve length generalization, these proposals typically apply to a limited set of tasks. Building on prior scratchpad and Chain-of-Thought (CoT) techniques, we propose Turing Programs, a novel CoT strategy that decomposes an algorithmic task into steps mimicking the computation of a Turing Machine. This framework is both universal, as it can accommodate any algorithmic task, and simple, requiring only copying text from the context with small modifications. We show that by using Turing Programs, we obtain robust length generalization on a range of algorithmic tasks: addition, multiplication and in-context SGD. We then demonstrate that transformers achieve length generalization on random Turing Programs, suggesting that length generalization is possible for any algorithmic task. Finally, we theoretically prove that transformers can implement Turing Programs, constructing a simple RASP (Weiss et al.) program that simulates an arbitrary Turing machine.

How Does Overparameterization Affect Features?

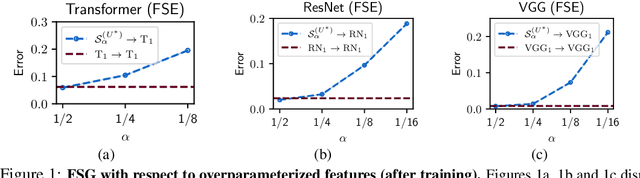
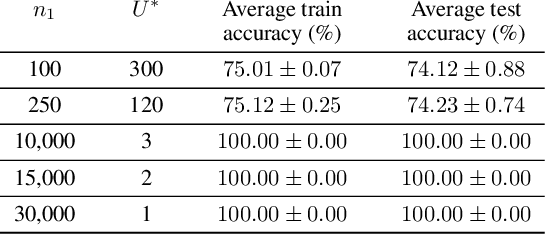
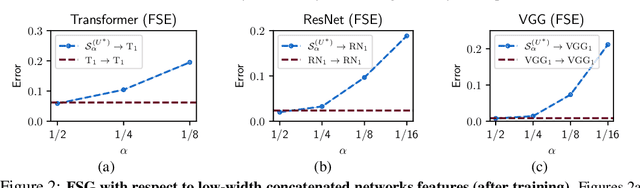
Overparameterization, the condition where models have more parameters than necessary to fit their training loss, is a crucial factor for the success of deep learning. However, the characteristics of the features learned by overparameterized networks are not well understood. In this work, we explore this question by comparing models with the same architecture but different widths. We first examine the expressivity of the features of these models, and show that the feature space of overparameterized networks cannot be spanned by concatenating many underparameterized features, and vice versa. This reveals that both overparameterized and underparameterized networks acquire some distinctive features. We then evaluate the performance of these models, and find that overparameterized networks outperform underparameterized networks, even when many of the latter are concatenated. We corroborate these findings using a VGG-16 and ResNet18 on CIFAR-10 and a Transformer on the MNLI classification dataset. Finally, we propose a toy setting to explain how overparameterized networks can learn some important features that the underparamaterized networks cannot learn.