From Static to Adaptive Defense: Federated Multi-Agent Deep Reinforcement Learning-Driven Moving Target Defense Against DoS Attacks in UAV Swarm Networks

The proliferation of unmanned aerial vehicle (UAV) swarms has enabled a wide range of mission-critical applications, but also exposes UAV networks to severe Denial-of-Service (DoS) threats due to their open wireless environment, dynamic topology, and resource constraints. Traditional static or centralized defense mechanisms are often inadequate for such dynamic and distributed scenarios. To address these challenges, we propose a novel federated multi-agent deep reinforcement learning (FMADRL)-driven moving target defense (MTD) framework for proactive and adaptive DoS mitigation in UAV swarm networks. Specifically, we design three lightweight and coordinated MTD mechanisms, including leader switching, route mutation, and frequency hopping, that leverage the inherent flexibility of UAV swarms to disrupt attacker efforts and enhance network resilience. The defense problem is formulated as a multi-agent partially observable Markov decision process (POMDP), capturing the distributed, resource-constrained, and uncertain nature of UAV swarms under attack. Each UAV is equipped with a local policy agent that autonomously selects MTD actions based on partial observations and local experiences. By employing a policy gradient-based FMADRL algorithm, UAVs collaboratively optimize their defense policies via reward-weighted aggregation, enabling distributed learning without sharing raw data and thus reducing communication overhead. Extensive simulations demonstrate that our approach significantly outperforms state-of-the-art baselines, achieving up to a 34.6% improvement in attack mitigation rate, a reduction in average recovery time of up to 94.6%, and decreases in energy consumption and defense cost by as much as 29.3% and 98.3%, respectively, while maintaining robust mission continuity under various DoS attack strategies.

Decomposing Elements of Problem Solving: What "Math" Does RL Teach?

Mathematical reasoning tasks have become prominent benchmarks for assessing the reasoning capabilities of LLMs, especially with reinforcement learning (RL) methods such as GRPO showing significant performance gains. However, accuracy metrics alone do not support fine-grained assessment of capabilities and fail to reveal which problem-solving skills have been internalized. To better understand these capabilities, we propose to decompose problem solving into fundamental capabilities: Plan (mapping questions to sequences of steps), Execute (correctly performing solution steps), and Verify (identifying the correctness of a solution). Empirically, we find that GRPO mainly enhances the execution skill-improving execution robustness on problems the model already knows how to solve-a phenomenon we call temperature distillation. More importantly, we show that RL-trained models struggle with fundamentally new problems, hitting a 'coverage wall' due to insufficient planning skills. To explore RL's impact more deeply, we construct a minimal, synthetic solution-tree navigation task as an analogy for mathematical problem-solving. This controlled setup replicates our empirical findings, confirming RL primarily boosts execution robustness. Importantly, in this setting, we identify conditions under which RL can potentially overcome the coverage wall through improved exploration and generalization to new solution paths. Our findings provide insights into the role of RL in enhancing LLM reasoning, expose key limitations, and suggest a path toward overcoming these barriers. Code is available at https://github.com/cfpark00/RL-Wall.

To Backtrack or Not to Backtrack: When Sequential Search Limits Model Reasoning

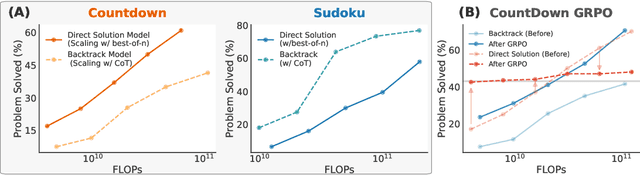
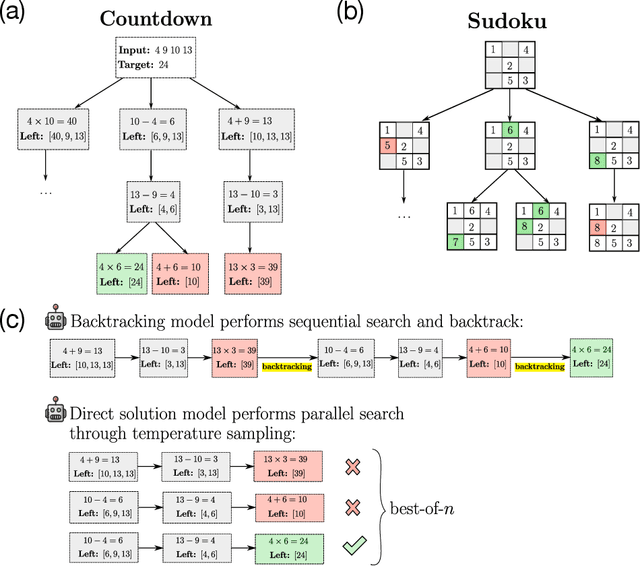
Recent advancements in large language models have significantly improved their reasoning abilities, particularly through techniques involving search and backtracking. Backtracking naturally scales test-time compute by enabling sequential, linearized exploration via long chain-of-thought (CoT) generation. However, this is not the only strategy for scaling test-time compute: parallel sampling with best-of-n selection provides an alternative that generates diverse solutions simultaneously. Despite the growing adoption of sequential search, its advantages over parallel sampling--especially under a fixed compute budget remain poorly understood. In this paper, we systematically compare these two approaches on two challenging reasoning tasks: CountDown and Sudoku. Surprisingly, we find that sequential search underperforms parallel sampling on CountDown but outperforms it on Sudoku, suggesting that backtracking is not universally beneficial. We identify two factors that can cause backtracking to degrade performance: (1) training on fixed search traces can lock models into suboptimal strategies, and (2) explicit CoT supervision can discourage "implicit" (non-verbalized) reasoning. Extending our analysis to reinforcement learning (RL), we show that models with backtracking capabilities benefit significantly from RL fine-tuning, while models without backtracking see limited, mixed gains. Together, these findings challenge the assumption that backtracking universally enhances LLM reasoning, instead revealing a complex interaction between task structure, training data, model scale, and learning paradigm.

Debiasing Kernel-Based Generative Models

We propose a novel two-stage framework of generative models named Debiasing Kernel-Based Generative Models (DKGM) with the insights from kernel density estimation (KDE) and stochastic approximation. In the first stage of DKGM, we employ KDE to bypass the obstacles in estimating the density of data without losing too much image quality. One characteristic of KDE is oversmoothing, which makes the generated image blurry. Therefore, in the second stage, we formulate the process of reducing the blurriness of images as a statistical debiasing problem and develop a novel iterative algorithm to improve image quality, which is inspired by the stochastic approximation. Extensive experiments illustrate that the image quality of DKGM on CIFAR10 is comparable to state-of-the-art models such as diffusion models and GAN models. The performance of DKGM on CelebA 128x128 and LSUN (Church) 128x128 is also competitive. We conduct extra experiments to exploit how the bandwidth in KDE affects the sample diversity and debiasing effect of DKGM. The connections between DKGM and score-based models are also discussed.

Distributional Scaling Laws for Emergent Capabilities

In this paper, we explore the nature of sudden breakthroughs in language model performance at scale, which stands in contrast to smooth improvements governed by scaling laws. While advocates of "emergence" view abrupt performance gains as capabilities unlocking at specific scales, others have suggested that they are produced by thresholding effects and alleviated by continuous metrics. We propose that breakthroughs are instead driven by continuous changes in the probability distribution of training outcomes, particularly when performance is bimodally distributed across random seeds. In synthetic length generalization tasks, we show that different random seeds can produce either highly linear or emergent scaling trends. We reveal that sharp breakthroughs in metrics are produced by underlying continuous changes in their distribution across seeds. Furthermore, we provide a case study of inverse scaling and show that even as the probability of a successful run declines, the average performance of a successful run continues to increase monotonically. We validate our distributional scaling framework on realistic settings by measuring MMLU performance in LLM populations. These insights emphasize the role of random variation in the effect of scale on LLM capabilities.

Sometimes I am a Tree: Data Drives Unstable Hierarchical Generalization

Neural networks often favor shortcut heuristics based on surface-level patterns. As one example, language models (LMs) behave like n-gram models early in training. However, to correctly apply grammatical rules, LMs must rely on hierarchical syntactic representations instead of n-grams. In this work, we use cases studies of English grammar to explore how latent structure in training data drives models toward improved out-of-distribution (OOD) generalization.We then investigate how data composition can lead to inconsistent OOD behavior across random seeds and to unstable training dynamics. Our results show that models stabilize in their OOD behavior only when they fully commit to either a surface-level linear rule or a hierarchical rule. The hierarchical rule, furthermore, is induced by grammatically complex sequences with deep embedding structures, whereas the linear rule is induced by simpler sequences. When the data contains a mix of simple and complex examples, potential rules compete; each independent training run either stabilizes by committing to a single rule or remains unstable in its OOD behavior. These conditions lead `stable seeds' to cluster around simple rules, forming bimodal performance distributions across seeds. We also identify an exception to the relationship between stability and generalization: models which memorize patterns from low-diversity training data can overfit stably, with different rules for memorized and unmemorized patterns. Our findings emphasize the critical role of training data in shaping generalization patterns and how competition between data subsets contributes to inconsistent generalization outcomes across random seeds. Code is available at https://github.com/sunnytqin/concept_comp.git.

A Label is Worth a Thousand Images in Dataset Distillation

Data $\textit{quality}$ is a crucial factor in the performance of machine learning models, a principle that dataset distillation methods exploit by compressing training datasets into much smaller counterparts that maintain similar downstream performance. Understanding how and why data distillation methods work is vital not only for improving these methods but also for revealing fundamental characteristics of "good" training data. However, a major challenge in achieving this goal is the observation that distillation approaches, which rely on sophisticated but mostly disparate methods to generate synthetic data, have little in common with each other. In this work, we highlight a largely overlooked aspect common to most of these methods: the use of soft (probabilistic) labels. Through a series of ablation experiments, we study the role of soft labels in depth. Our results reveal that the main factor explaining the performance of state-of-the-art distillation methods is not the specific techniques used to generate synthetic data but rather the use of soft labels. Furthermore, we demonstrate that not all soft labels are created equal; they must contain $\textit{structured information}$ to be beneficial. We also provide empirical scaling laws that characterize the effectiveness of soft labels as a function of images-per-class in the distilled dataset and establish an empirical Pareto frontier for data-efficient learning. Combined, our findings challenge conventional wisdom in dataset distillation, underscore the importance of soft labels in learning, and suggest new directions for improving distillation methods. Code for all experiments is available at https://github.com/sunnytqin/no-distillation.

Epanechnikov Variational Autoencoder

In this paper, we bridge Variational Autoencoders (VAEs) [17] and kernel density estimations (KDEs) [25 ],[23] by approximating the posterior by KDEs and deriving an upper bound of the Kullback-Leibler (KL) divergence in the evidence lower bound (ELBO). The flexibility of KDEs makes the optimization of posteriors in VAEs possible, which not only addresses the limitations of Gaussian latent space in vanilla VAE but also provides a new perspective of estimating the KL-divergence in ELBO. Under appropriate conditions [ 9],[3 ], we show that the Epanechnikov kernel is the optimal choice in minimizing the derived upper bound of KL-divergence asymptotically. Compared with Gaussian kernel, Epanechnikov kernel has compact support which should make the generated sample less noisy and blurry. The implementation of Epanechnikov kernel in ELBO is straightforward as it lies in the "location-scale" family of distributions where the reparametrization tricks can be directly employed. A series of experiments on benchmark datasets such as MNIST, Fashion-MNIST, CIFAR-10 and CelebA further demonstrate the superiority of Epanechnikov Variational Autoenocoder (EVAE) over vanilla VAE in the quality of reconstructed images, as measured by the FID score and Sharpness[27].

Distributional Dataset Distillation with Subtask Decomposition

What does a neural network learn when training from a task-specific dataset? Synthesizing this knowledge is the central idea behind Dataset Distillation, which recent work has shown can be used to compress large datasets into a small set of input-label pairs ($\textit{prototypes}$) that capture essential aspects of the original dataset. In this paper, we make the key observation that existing methods distilling into explicit prototypes are very often suboptimal, incurring in unexpected storage cost from distilled labels. In response, we propose $\textit{Distributional Dataset Distillation}$ (D3), which encodes the data using minimal sufficient per-class statistics and paired with a decoder, we distill dataset into a compact distributional representation that is more memory-efficient compared to prototype-based methods. To scale up the process of learning these representations, we propose $\textit{Federated distillation}$, which decomposes the dataset into subsets, distills them in parallel using sub-task experts and then re-aggregates them. We thoroughly evaluate our algorithm on a three-dimensional metric and show that our method achieves state-of-the-art results on TinyImageNet and ImageNet-1K. Specifically, we outperform the prior art by $6.9\%$ on ImageNet-1K under the storage budget of 2 images per class.

Riemann-Lebesgue Forest for Regression

We propose a novel ensemble method called Riemann-Lebesgue Forest (RLF) for regression. The core idea of RLF is to mimic the way how a measurable function can be approximated by partitioning its range into a few intervals. With this idea in mind, we develop a new tree learner named Riemann-Lebesgue Tree which has a chance to split the node from response $Y$ or a direction in feature space $\mathbf{X}$ at each non-terminal node. We generalize the asymptotic performance of RLF under different parameter settings mainly through Hoeffding decomposition \cite{Vaart} and Stein's method \cite{Chen2010NormalAB}. When the underlying function $Y=f(\mathbf{X})$ follows an additive regression model, RLF is consistent with the argument from \cite{Scornet2014ConsistencyOR}. The competitive performance of RLF against original random forest \cite{Breiman2001RandomF} is demonstrated by experiments in simulation data and real world datasets.