Budgeted Multiple-Expert Deferral

Learning to defer uncertain predictions to costly experts offers a powerful strategy for improving the accuracy and efficiency of machine learning systems. However, standard training procedures for deferral algorithms typically require querying all experts for every training instance, an approach that becomes prohibitively expensive when expert queries incur significant computational or resource costs. This undermines the core goal of deferral: to limit unnecessary expert usage. To overcome this challenge, we introduce the budgeted deferral framework, which aims to train effective deferral algorithms while minimizing expert query costs during training. We propose new algorithms for both two-stage and single-stage multiple-expert deferral settings that selectively query only a subset of experts per training example. While inspired by active learning, our setting is fundamentally different: labels are already known, and the core challenge is to decide which experts to query in order to balance cost and predictive performance. We establish theoretical guarantees for both of our algorithms, including generalization bounds and label complexity analyses. Empirical results across several domains show that our algorithms substantially reduce training costs without sacrificing prediction accuracy, demonstrating the practical value of our budget-aware deferral algorithms.

Mixture of Parrots: Experts improve memorization more than reasoning

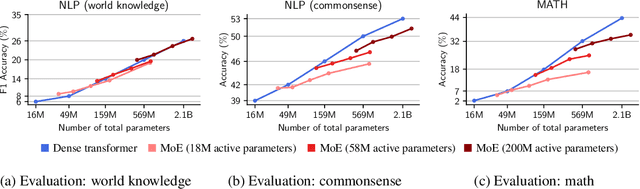
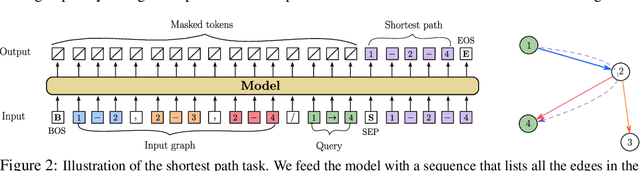
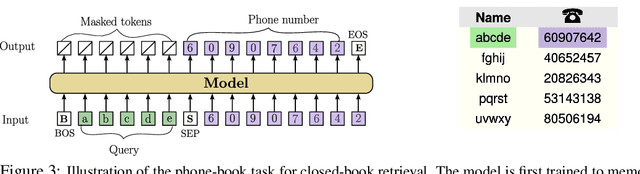
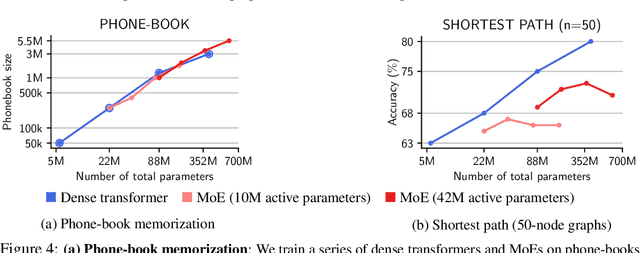
The Mixture-of-Experts (MoE) architecture enables a significant increase in the total number of model parameters with minimal computational overhead. However, it is not clear what performance tradeoffs, if any, exist between MoEs and standard dense transformers. In this paper, we show that as we increase the number of experts (while fixing the number of active parameters), the memorization performance consistently increases while the reasoning capabilities saturate. We begin by analyzing the theoretical limitations of MoEs at reasoning. We prove that there exist graph problems that cannot be solved by any number of experts of a certain width; however, the same task can be easily solved by a dense model with a slightly larger width. On the other hand, we find that on memory-intensive tasks, MoEs can effectively leverage a small number of active parameters with a large number of experts to memorize the data. We empirically validate these findings on synthetic graph problems and memory-intensive closed book retrieval tasks. Lastly, we pre-train a series of MoEs and dense transformers and evaluate them on commonly used benchmarks in math and natural language. We find that increasing the number of experts helps solve knowledge-intensive tasks, but fails to yield the same benefits for reasoning tasks.

Using Language to Extend to Unseen Domains

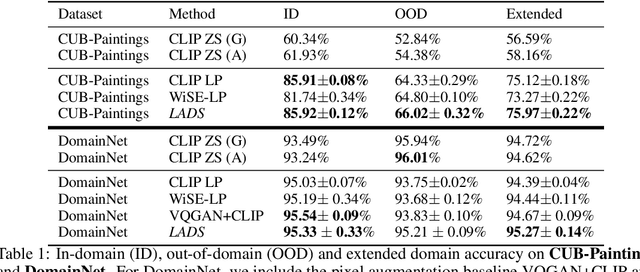
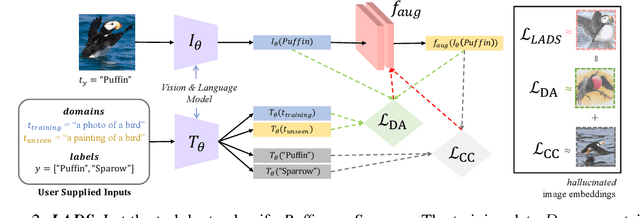
It is expensive to collect training data for every possible domain that a vision model may encounter when deployed. We instead consider how simply verbalizing the training domain (e.g. "photos of birds") as well as domains we want to extend to but do not have data for (e.g. "paintings of birds") can improve robustness. Using a multimodal model with a joint image and language embedding space, our method LADS learns a transformation of the image embeddings from the training domain to each unseen test domain, while preserving task relevant information. Without using any images from the unseen test domain, we show that over the extended domain containing both training and unseen test domains, LADS outperforms standard fine-tuning and ensemble approaches over a suite of four benchmarks targeting domain adaptation and dataset bias