Forecasting Generative Amplification

Generative networks are perfect tools to enhance the speed and precision of LHC simulations. It is important to understand their statistical precision, especially when generating events beyond the size of the training dataset. We present two complementary methods to estimate the amplification factor without large holdout datasets. Averaging amplification uses Bayesian networks or ensembling to estimate amplification from the precision of integrals over given phase-space volumes. Differential amplification uses hypothesis testing to quantify amplification without any resolution loss. Applied to state-of-the-art event generators, both methods indicate that amplification is possible in specific regions of phase space, but not yet across the entire distribution.

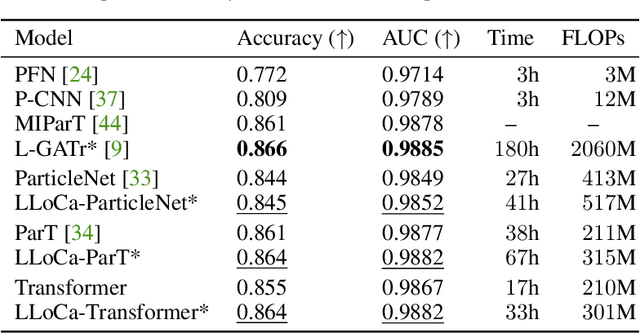
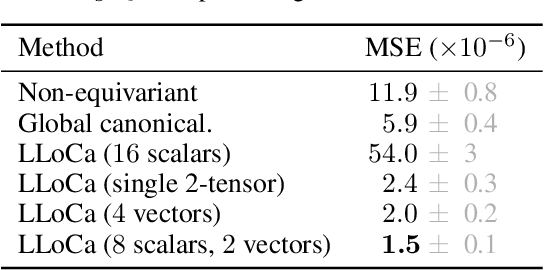
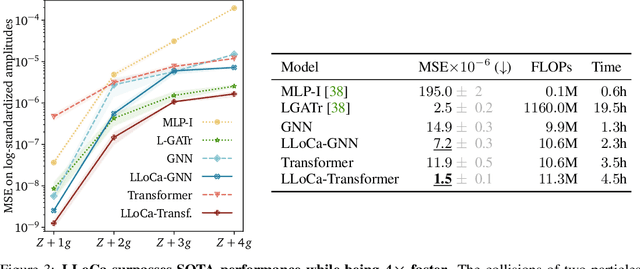
Lorentz Local Canonicalization: How to Make Any Network Lorentz-Equivariant

Lorentz-equivariant neural networks are becoming the leading architectures for high-energy physics. Current implementations rely on specialized layers, limiting architectural choices. We introduce Lorentz Local Canonicalization (LLoCa), a general framework that renders any backbone network exactly Lorentz-equivariant. Using equivariantly predicted local reference frames, we construct LLoCa-transformers and graph networks. We adapt a recent approach to geometric message passing to the non-compact Lorentz group, allowing propagation of space-time tensorial features. Data augmentation emerges from LLoCa as a special choice of reference frame. Our models surpass state-of-the-art accuracy on relevant particle physics tasks, while being $4\times$ faster and using $5$-$100\times$ fewer FLOPs.

Extrapolating Jet Radiation with Autoregressive Transformers

Generative networks are an exciting tool for fast LHC event generation. Usually, they are used to generate configurations with a fixed number of particles. Autoregressive transformers allow us to generate events with variable numbers of particles, very much in line with the physics of QCD jet radiation. We show how they can learn a factorized likelihood for jet radiation and extrapolate in terms of the number of generated jets. For this extrapolation, bootstrapping training data and training with modifications of the likelihood loss can be used.

Generative Unfolding with Distribution Mapping

Machine learning enables unbinned, highly-differential cross section measurements. A recent idea uses generative models to morph a starting simulation into the unfolded data. We show how to extend two morphing techniques, Schr\"odinger Bridges and Direct Diffusion, in order to ensure that the models learn the correct conditional probabilities. This brings distribution mapping to a similar level of accuracy as the state-of-the-art conditional generative unfolding methods. Numerical results are presented with a standard benchmark dataset of single jet substructure as well as for a new dataset describing a 22-dimensional phase space of Z + 2-jets.

A Lorentz-Equivariant Transformer for All of the LHC

We show that the Lorentz-Equivariant Geometric Algebra Transformer (L-GATr) yields state-of-the-art performance for a wide range of machine learning tasks at the Large Hadron Collider. L-GATr represents data in a geometric algebra over space-time and is equivariant under Lorentz transformations. The underlying architecture is a versatile and scalable transformer, which is able to break symmetries if needed. We demonstrate the power of L-GATr for amplitude regression and jet classification, and then benchmark it as the first Lorentz-equivariant generative network. For all three LHC tasks, we find significant improvements over previous architectures.

CaloChallenge 2022: A Community Challenge for Fast Calorimeter Simulation

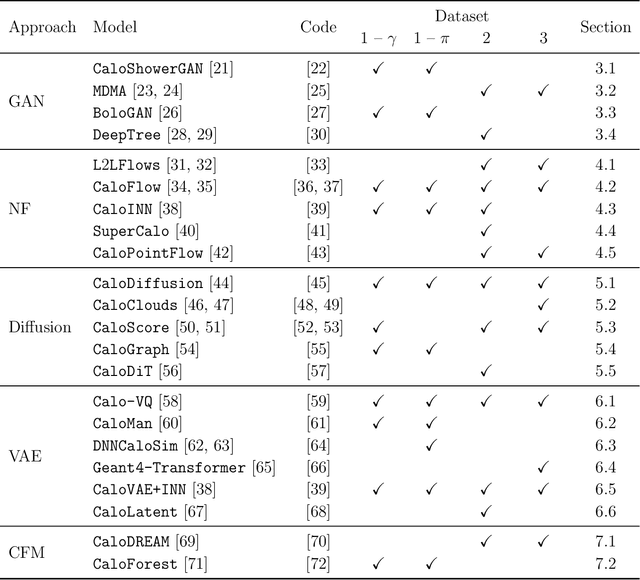
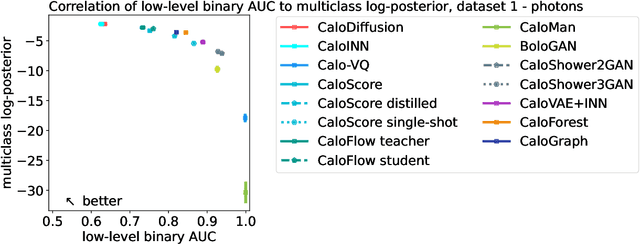
We present the results of the "Fast Calorimeter Simulation Challenge 2022" - the CaloChallenge. We study state-of-the-art generative models on four calorimeter shower datasets of increasing dimensionality, ranging from a few hundred voxels to a few tens of thousand voxels. The 31 individual submissions span a wide range of current popular generative architectures, including Variational AutoEncoders (VAEs), Generative Adversarial Networks (GANs), Normalizing Flows, Diffusion models, and models based on Conditional Flow Matching. We compare all submissions in terms of quality of generated calorimeter showers, as well as shower generation time and model size. To assess the quality we use a broad range of different metrics including differences in 1-dimensional histograms of observables, KPD/FPD scores, AUCs of binary classifiers, and the log-posterior of a multiclass classifier. The results of the CaloChallenge provide the most complete and comprehensive survey of cutting-edge approaches to calorimeter fast simulation to date. In addition, our work provides a uniquely detailed perspective on the important problem of how to evaluate generative models. As such, the results presented here should be applicable for other domains that use generative AI and require fast and faithful generation of samples in a large phase space.

Constraining the Higgs Potential with Neural Simulation-based Inference for Di-Higgs Production

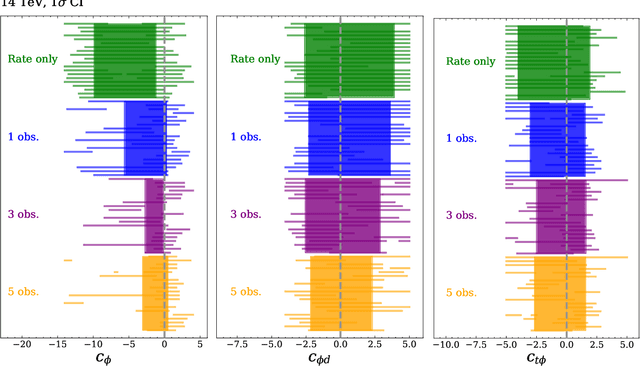
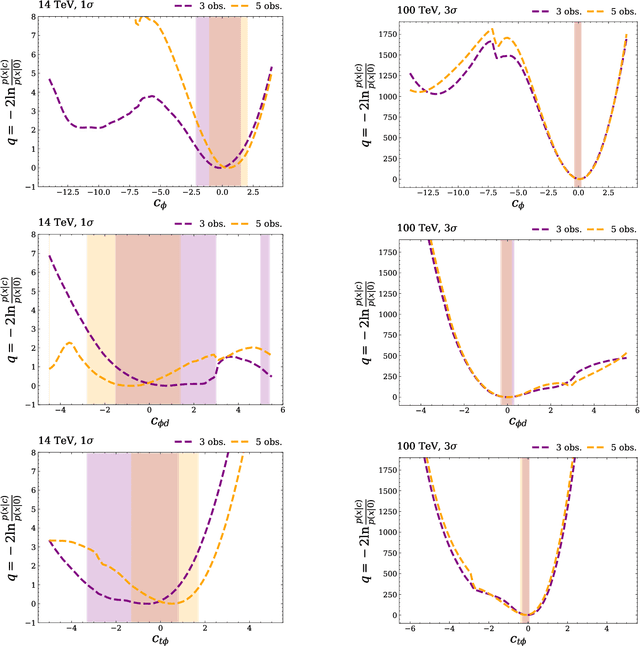
Determining the form of the Higgs potential is one of the most exciting challenges of modern particle physics. Higgs pair production directly probes the Higgs self-coupling and should be observed in the near future at the High-Luminosity LHC. We explore how to improve the sensitivity to physics beyond the Standard Model through per-event kinematics for di-Higgs events. In particular, we employ machine learning through simulation-based inference to estimate per-event likelihood ratios and gauge potential sensitivity gains from including this kinematic information. In terms of the Standard Model Effective Field Theory, we find that adding a limited number of observables can help to remove degeneracies in Wilson coefficient likelihoods and significantly improve the experimental sensitivity.

Lorentz-Equivariant Geometric Algebra Transformers for High-Energy Physics

Extracting scientific understanding from particle-physics experiments requires solving diverse learning problems with high precision and good data efficiency. We propose the Lorentz Geometric Algebra Transformer (L-GATr), a new multi-purpose architecture for high-energy physics. L-GATr represents high-energy data in a geometric algebra over four-dimensional space-time and is equivariant under Lorentz transformations, the symmetry group of relativistic kinematics. At the same time, the architecture is a Transformer, which makes it versatile and scalable to large systems. L-GATr is first demonstrated on regression and classification tasks from particle physics. We then construct the first Lorentz-equivariant generative model: a continuous normalizing flow based on an L-GATr network, trained with Riemannian flow matching. Across our experiments, L-GATr is on par with or outperforms strong domain-specific baselines.

The Landscape of Unfolding with Machine Learning

Recent innovations from machine learning allow for data unfolding, without binning and including correlations across many dimensions. We describe a set of known, upgraded, and new methods for ML-based unfolding. The performance of these approaches are evaluated on the same two datasets. We find that all techniques are capable of accurately reproducing the particle-level spectra across complex observables. Given that these approaches are conceptually diverse, they offer an exciting toolkit for a new class of measurements that can probe the Standard Model with an unprecedented level of detail and may enable sensitivity to new phenomena.

Anomalies, Representations, and Self-Supervision

We develop a self-supervised method for density-based anomaly detection using contrastive learning, and test it using event-level anomaly data from CMS ADC2021. The AnomalyCLR technique is data-driven and uses augmentations of the background data to mimic non-Standard-Model events in a model-agnostic way. It uses a permutation-invariant Transformer Encoder architecture to map the objects measured in a collider event to the representation space, where the data augmentations define a representation space which is sensitive to potential anomalous features. An AutoEncoder trained on background representations then computes anomaly scores for a variety of signals in the representation space. With AnomalyCLR we find significant improvements on performance metrics for all signals when compared to the raw data baseline.