Tensor Frames -- How To Make Any Message Passing Network Equivariant

In many applications of geometric deep learning, the choice of global coordinate frame is arbitrary, and predictions should be independent of the reference frame. In other words, the network should be equivariant with respect to rotations and reflections of the input, i.e., the transformations of O(d). We present a novel framework for building equivariant message passing architectures and modifying existing non-equivariant architectures to be equivariant. Our approach is based on local coordinate frames, between which geometric information is communicated consistently by including tensorial objects in the messages. Our framework can be applied to message passing on geometric data in arbitrary dimensional Euclidean space. While many other approaches for equivariant message passing require specialized building blocks, such as non-standard normalization layers or non-linearities, our approach can be adapted straightforwardly to any existing architecture without such modifications. We explicitly demonstrate the benefit of O(3)-equivariance for a popular point cloud architecture and produce state-of-the-art results on normal vector regression on point clouds.

Theory and Approximate Solvers for Branched Optimal Transport with Multiple Sources

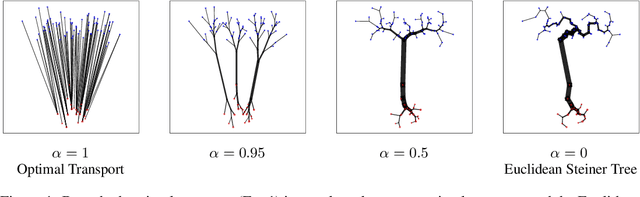
Branched Optimal Transport (BOT) is a generalization of optimal transport in which transportation costs along an edge are subadditive. This subadditivity models an increase in transport efficiency when shipping mass along the same route, favoring branched transportation networks. We here study the NP-hard optimization of BOT networks connecting a finite number of sources and sinks in $\mathbb{R}^2$. First, we show how to efficiently find the best geometry of a BOT network for many sources and sinks, given a topology. Second, we argue that a topology with more than three edges meeting at a branching point is never optimal. Third, we show that the results obtained for the Euclidean plane generalize directly to optimal transportation networks on two-dimensional Riemannian manifolds. Finally, we present a simple but effective approximate BOT solver combining geometric optimization with a combinatorial optimization of the network topology.