The Central Spanning Tree Problem

Spanning trees are an important primitive in many data analysis tasks, when a data set needs to be summarized in terms of its "skeleton", or when a tree-shaped graph over all observations is required for downstream processing. Popular definitions of spanning trees include the minimum spanning tree and the optimum distance spanning tree, a.k.a. the minimum routing cost tree. When searching for the shortest spanning tree but admitting additional branching points, even shorter spanning trees can be realized: Steiner trees. Unfortunately, both minimum spanning and Steiner trees are not robust with respect to noise in the observations; that is, small perturbations of the original data set often lead to drastic changes in the associated spanning trees. In response, we make two contributions when the data lies in a Euclidean space: on the theoretical side, we introduce a new optimization problem, the "(branched) central spanning tree", which subsumes all previously mentioned definitions as special cases. On the practical side, we show empirically that the (branched) central spanning tree is more robust to noise in the data, and as such is better suited to summarize a data set in terms of its skeleton. We also propose a heuristic to address the NP-hard optimization problem, and illustrate its use on single cell RNA expression data from biology and 3D point clouds of plants.

Theory and Approximate Solvers for Branched Optimal Transport with Multiple Sources

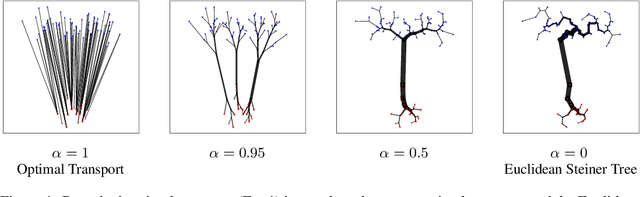
Branched Optimal Transport (BOT) is a generalization of optimal transport in which transportation costs along an edge are subadditive. This subadditivity models an increase in transport efficiency when shipping mass along the same route, favoring branched transportation networks. We here study the NP-hard optimization of BOT networks connecting a finite number of sources and sinks in $\mathbb{R}^2$. First, we show how to efficiently find the best geometry of a BOT network for many sources and sinks, given a topology. Second, we argue that a topology with more than three edges meeting at a branching point is never optimal. Third, we show that the results obtained for the Euclidean plane generalize directly to optimal transportation networks on two-dimensional Riemannian manifolds. Finally, we present a simple but effective approximate BOT solver combining geometric optimization with a combinatorial optimization of the network topology.

Extensions of Karger's Algorithm: Why They Fail in Theory and How They Are Useful in Practice

The minimum graph cut and minimum $s$-$t$-cut problems are important primitives in the modeling of combinatorial problems in computer science, including in computer vision and machine learning. Some of the most efficient algorithms for finding global minimum cuts are randomized algorithms based on Karger's groundbreaking contraction algorithm. Here, we study whether Karger's algorithm can be successfully generalized to other cut problems. We first prove that a wide class of natural generalizations of Karger's algorithm cannot efficiently solve the $s$-$t$-mincut or the normalized cut problem to optimality. However, we then present a simple new algorithm for seeded segmentation / graph-based semi-supervised learning that is closely based on Karger's original algorithm, showing that for these problems, extensions of Karger's algorithm can be useful. The new algorithm has linear asymptotic runtime and yields a potential that can be interpreted as the posterior probability of a sample belonging to a given seed / class. We clarify its relation to the random walker algorithm / harmonic energy minimization in terms of distributions over spanning forests. On classical problems from seeded image segmentation and graph-based semi-supervised learning on image data, the method performs at least as well as the random walker / harmonic energy minimization / Gaussian processes.