Extrapolating Jet Radiation with Autoregressive Transformers

Generative networks are an exciting tool for fast LHC event generation. Usually, they are used to generate configurations with a fixed number of particles. Autoregressive transformers allow us to generate events with variable numbers of particles, very much in line with the physics of QCD jet radiation. We show how they can learn a factorized likelihood for jet radiation and extrapolate in terms of the number of generated jets. For this extrapolation, bootstrapping training data and training with modifications of the likelihood loss can be used.

Generative Unfolding with Distribution Mapping

Machine learning enables unbinned, highly-differential cross section measurements. A recent idea uses generative models to morph a starting simulation into the unfolded data. We show how to extend two morphing techniques, Schr\"odinger Bridges and Direct Diffusion, in order to ensure that the models learn the correct conditional probabilities. This brings distribution mapping to a similar level of accuracy as the state-of-the-art conditional generative unfolding methods. Numerical results are presented with a standard benchmark dataset of single jet substructure as well as for a new dataset describing a 22-dimensional phase space of Z + 2-jets.

The Landscape of Unfolding with Machine Learning

Recent innovations from machine learning allow for data unfolding, without binning and including correlations across many dimensions. We describe a set of known, upgraded, and new methods for ML-based unfolding. The performance of these approaches are evaluated on the same two datasets. We find that all techniques are capable of accurately reproducing the particle-level spectra across complex observables. Given that these approaches are conceptually diverse, they offer an exciting toolkit for a new class of measurements that can probe the Standard Model with an unprecedented level of detail and may enable sensitivity to new phenomena.

An unfolding method based on conditional Invertible Neural Networks (cINN) using iterative training

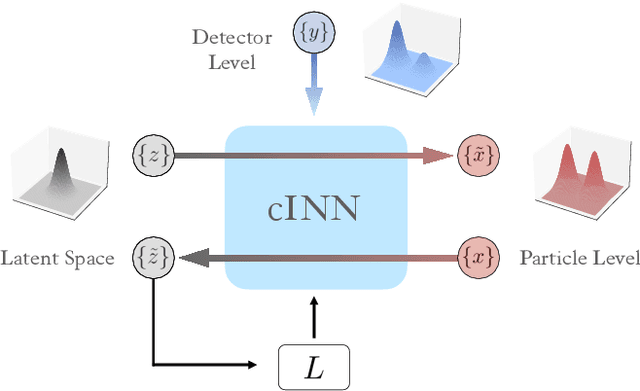
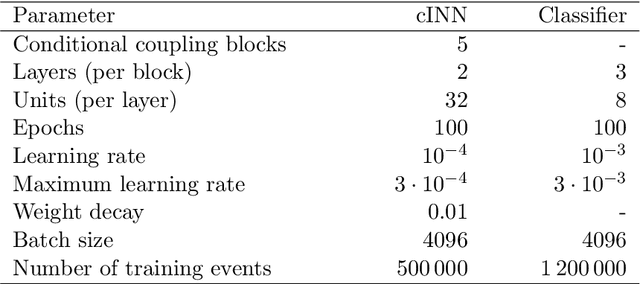
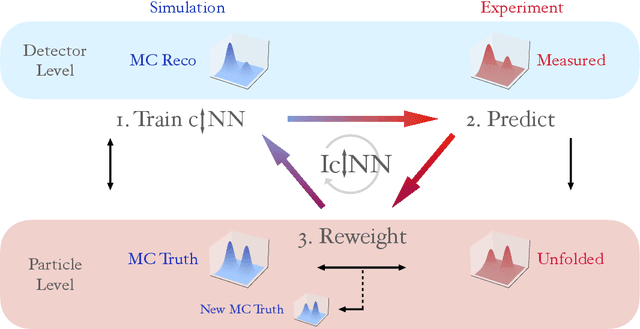
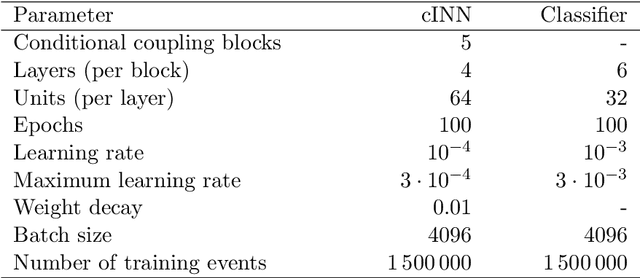
The unfolding of detector effects is crucial for the comparison of data to theory predictions. While traditional methods are limited to representing the data in a low number of dimensions, machine learning has enabled new unfolding techniques while retaining the full dimensionality. Generative networks like invertible neural networks~(INN) enable a probabilistic unfolding, which map individual events to their corresponding unfolded probability distribution. The accuracy of such methods is however limited by how well simulated training samples model the actual data that is unfolded. We introduce the iterative conditional INN~(IcINN) for unfolding that adjusts for deviations between simulated training samples and data. The IcINN unfolding is first validated on toy data and then applied to pseudo-data for the $pp \to Z \gamma \gamma$ process.

Generative Networks for Precision Enthusiasts

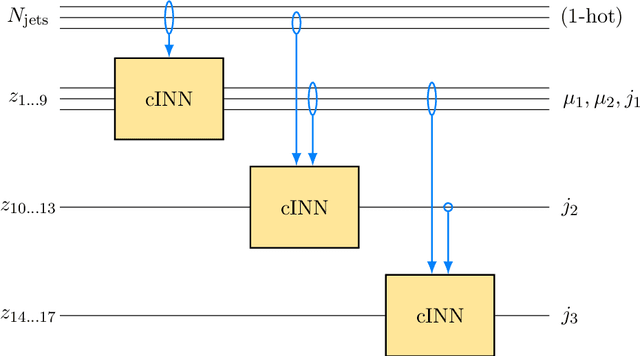
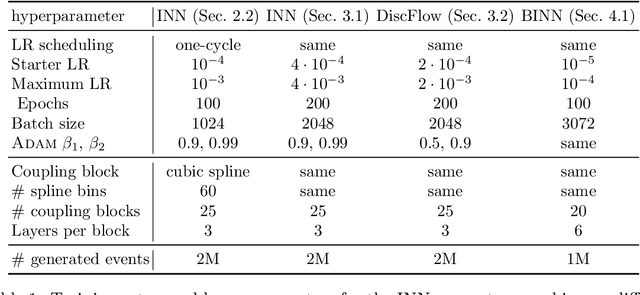
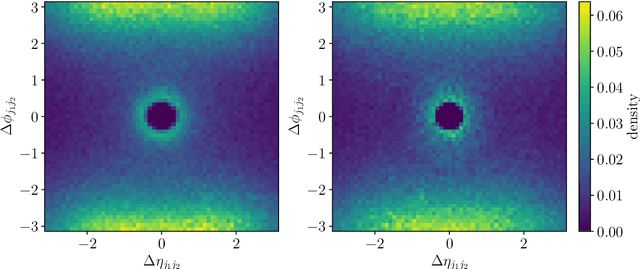
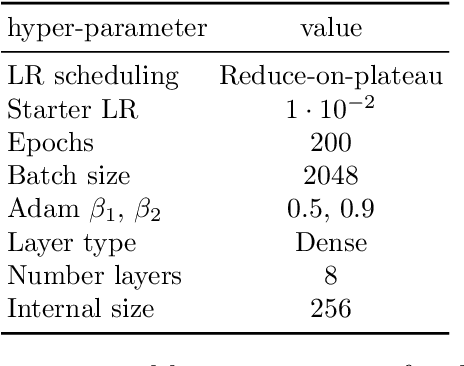
Generative networks are opening new avenues in fast event generation for the LHC. We show how generative flow networks can reach percent-level precision for kinematic distributions, how they can be trained jointly with a discriminator, and how this discriminator improves the generation. Our joint training relies on a novel coupling of the two networks which does not require a Nash equilibrium. We then estimate the generation uncertainties through a Bayesian network setup and through conditional data augmentation, while the discriminator ensures that there are no systematic inconsistencies compared to the training data.

GANplifying Event Samples

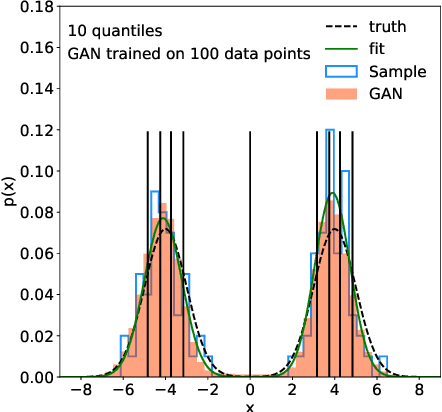
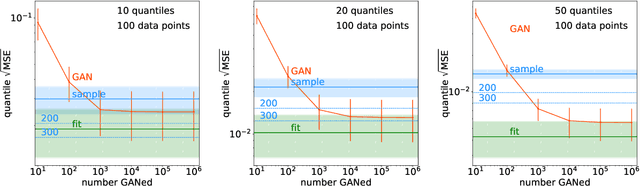
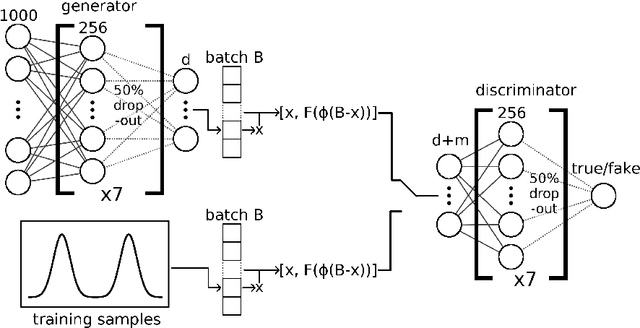
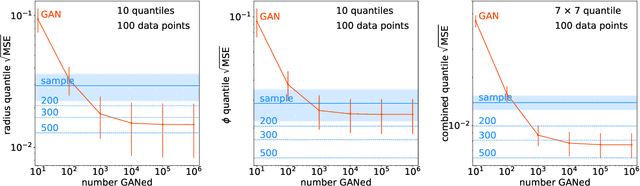
A critical question concerning generative networks applied to event generation in particle physics is if the generated events add statistical precision beyond the training sample. We show for a simple example with increasing dimensionality how generative networks indeed amplify the training statistics. We quantify their impact through an amplification factor or equivalent numbers of sampled events.