Learning Distributions on Manifolds with Free-form Flows

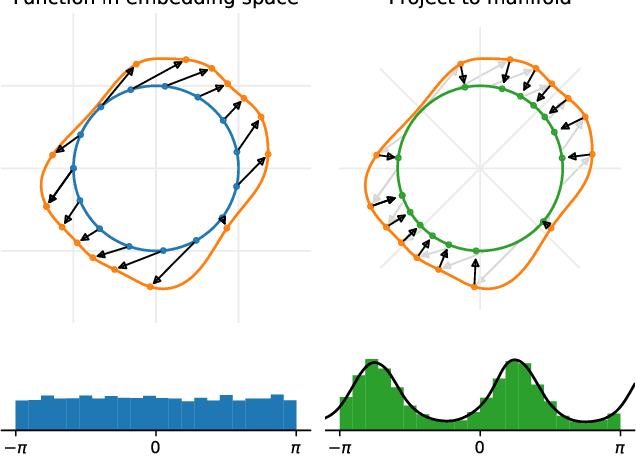
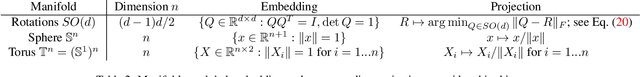
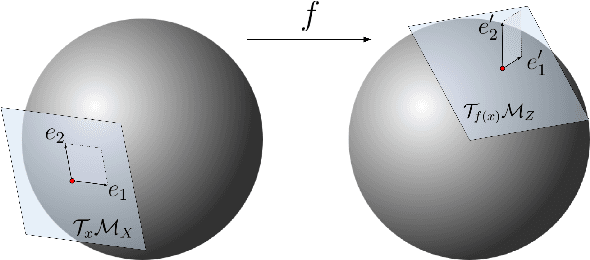
Many real world data, particularly in the natural sciences and computer vision, lie on known Riemannian manifolds such as spheres, tori or the group of rotation matrices. The predominant approaches to learning a distribution on such a manifold require solving a differential equation in order to sample from the model and evaluate densities. The resulting sampling times are slowed down by a high number of function evaluations. In this work, we propose an alternative approach which only requires a single function evaluation followed by a projection to the manifold. Training is achieved by an adaptation of the recently proposed free-form flow framework to Riemannian manifolds. The central idea is to estimate the gradient of the negative log-likelihood via a trace evaluated in the tangent space. We evaluate our method on various manifolds, and find significantly faster inference at competitive performance compared to previous work. We make our code public at https://github.com/vislearn/FFF.

Maximum Likelihood Training of Autoencoders

Maximum likelihood training has favorable statistical properties and is popular for generative modeling, especially with normalizing flows. On the other hand, generative autoencoders promise to be more efficient than normalizing flows due to the manifold hypothesis. In this work, we introduce successful maximum likelihood training of unconstrained autoencoders for the first time, bringing the two paradigms together. To do so, we identify and overcome two challenges: Firstly, existing maximum likelihood estimators for free-form networks are unacceptably slow, relying on iteration schemes whose cost scales linearly with latent dimension. We introduce an improved estimator which eliminates iteration, resulting in constant cost (roughly double the runtime per batch of a vanilla autoencoder). Secondly, we demonstrate that naively applying maximum likelihood to autoencoders can lead to divergent solutions and use this insight to motivate a stable maximum likelihood training objective. We perform extensive experiments on toy, tabular and image data, demonstrating the competitive performance of the resulting model. We call our model the maximum likelihood autoencoder (MLAE).

Generative Networks for Precision Enthusiasts

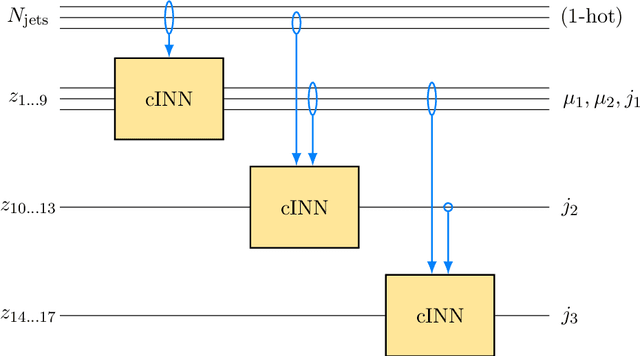
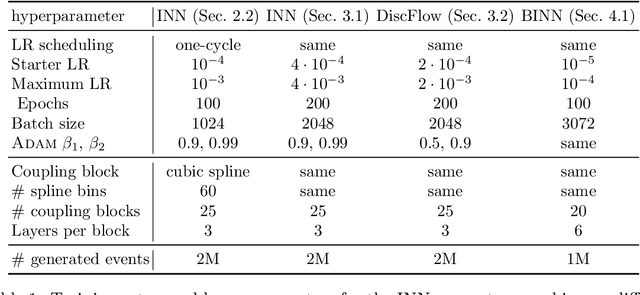
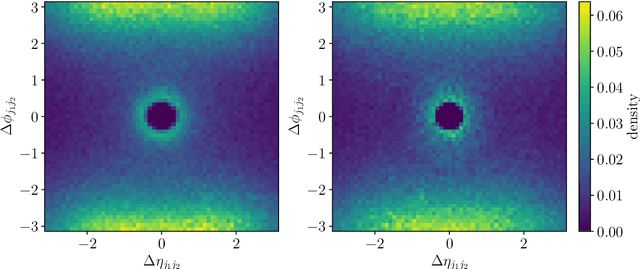
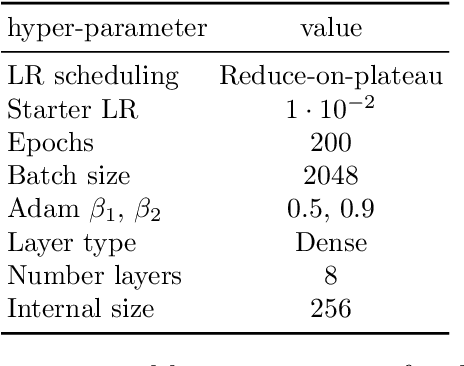
Generative networks are opening new avenues in fast event generation for the LHC. We show how generative flow networks can reach percent-level precision for kinematic distributions, how they can be trained jointly with a discriminator, and how this discriminator improves the generation. Our joint training relies on a novel coupling of the two networks which does not require a Nash equilibrium. We then estimate the generation uncertainties through a Bayesian network setup and through conditional data augmentation, while the discriminator ensures that there are no systematic inconsistencies compared to the training data.