Parallel Token Prediction for Language Models

We propose Parallel Token Prediction (PTP), a universal framework for parallel sequence generation in language models. PTP jointly predicts multiple dependent tokens in a single transformer call by incorporating the sampling procedure into the model. This reduces the latency bottleneck of autoregressive decoding, and avoids the restrictive independence assumptions common in existing multi-token prediction methods. We prove that PTP can represent arbitrary autoregressive sequence distributions. PTP is trained either by distilling an existing model or through inverse autoregressive training without a teacher. Experimentally, we achieve state-of-the-art speculative decoding performance on Vicuna-7B by accepting over four tokens per step on Spec-Bench. The universality of our framework indicates that parallel generation of long sequences is feasible without loss of modeling power.

Variational Control for Guidance in Diffusion Models

Diffusion models exhibit excellent sample quality, but existing guidance methods often require additional model training or are limited to specific tasks. We revisit guidance in diffusion models from the perspective of variational inference and control, introducing Diffusion Trajectory Matching (DTM) that enables guiding pretrained diffusion trajectories to satisfy a terminal cost. DTM unifies a broad class of guidance methods and enables novel instantiations. We introduce a new method within this framework that achieves state-of-the-art results on several linear and (blind) non-linear inverse problems without requiring additional model training or modifications. For instance, in ImageNet non-linear deblurring, our model achieves an FID score of 34.31, significantly improving over the best pretrained-method baseline (FID 78.07). We will make the code available in a future update.

TRADE: Transfer of Distributions between External Conditions with Normalizing Flows

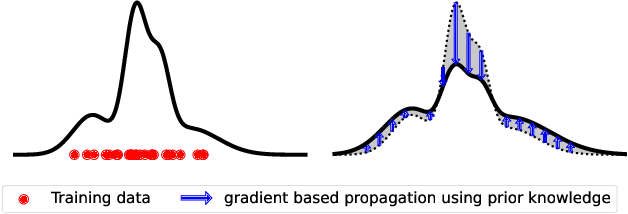
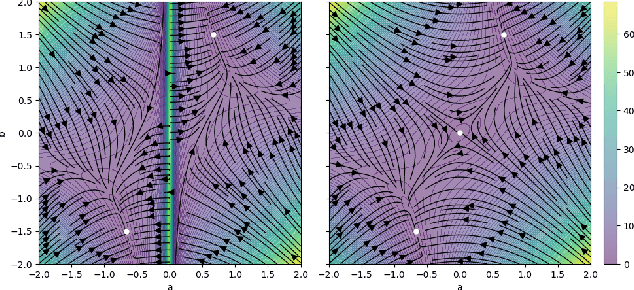
Modeling distributions that depend on external control parameters is a common scenario in diverse applications like molecular simulations, where system properties like temperature affect molecular configurations. Despite the relevance of these applications, existing solutions are unsatisfactory as they require severely restricted model architectures or rely on backward training, which is prone to unstable training. We introduce TRADE, which overcomes these limitations by formulating the learning process as a boundary value problem. By initially training the model for a specific condition using either i.i.d. samples or backward KL training, we establish a boundary distribution. We then propagate this information across other conditions using the gradient of the unnormalized density with respect to the external parameter. This formulation, akin to the principles of physics-informed neural networks, allows us to efficiently learn parameter-dependent distributions without restrictive assumptions. Experimentally, we demonstrate that TRADE achieves excellent results in a wide range of applications, ranging from Bayesian inference and molecular simulations to physical lattice models.

On the Universality of Coupling-based Normalizing Flows

We present a novel theoretical framework for understanding the expressive power of coupling-based normalizing flows such as RealNVP. Despite their prevalence in scientific applications, a comprehensive understanding of coupling flows remains elusive due to their restricted architectures. Existing theorems fall short as they require the use of arbitrarily ill-conditioned neural networks, limiting practical applicability. Additionally, we demonstrate that these constructions inherently lead to volume-preserving flows, a property which we show to be a fundamental constraint for expressivity. We propose a new distributional universality theorem for coupling-based normalizing flows, which overcomes several limitations of prior work. Our results support the general wisdom that the coupling architecture is expressive and provide a nuanced view for choosing the expressivity of coupling functions, bridging a gap between empirical results and theoretical understanding.

Learning Distributions on Manifolds with Free-form Flows

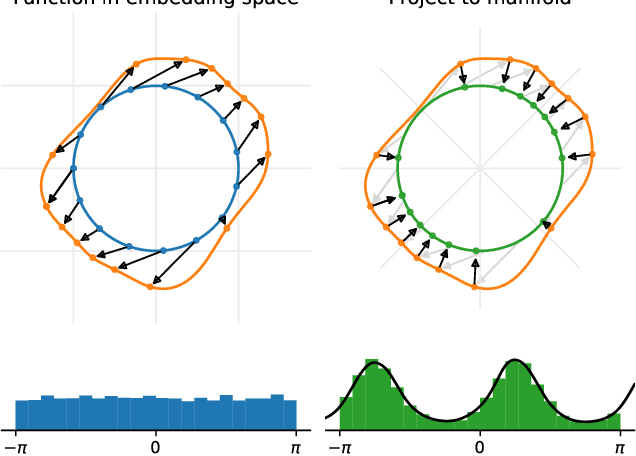
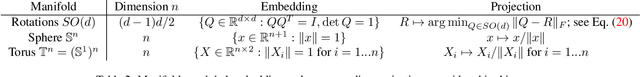
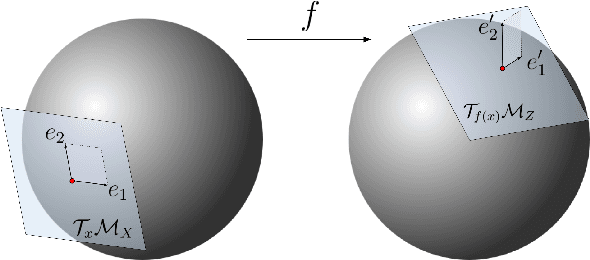
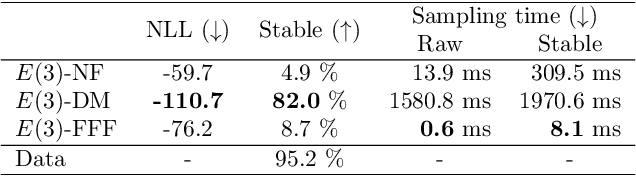
Many real world data, particularly in the natural sciences and computer vision, lie on known Riemannian manifolds such as spheres, tori or the group of rotation matrices. The predominant approaches to learning a distribution on such a manifold require solving a differential equation in order to sample from the model and evaluate densities. The resulting sampling times are slowed down by a high number of function evaluations. In this work, we propose an alternative approach which only requires a single function evaluation followed by a projection to the manifold. Training is achieved by an adaptation of the recently proposed free-form flow framework to Riemannian manifolds. The central idea is to estimate the gradient of the negative log-likelihood via a trace evaluated in the tangent space. We evaluate our method on various manifolds, and find significantly faster inference at competitive performance compared to previous work. We make our code public at https://github.com/vislearn/FFF.

Free-form Flows: Make Any Architecture a Normalizing Flow

Normalizing Flows are generative models that directly maximize the likelihood. Previously, the design of normalizing flows was largely constrained by the need for analytical invertibility. We overcome this constraint by a training procedure that uses an efficient estimator for the gradient of the change of variables formula. This enables any dimension-preserving neural network to serve as a generative model through maximum likelihood training. Our approach allows placing the emphasis on tailoring inductive biases precisely to the task at hand. Specifically, we achieve excellent results in molecule generation benchmarks utilizing $E(n)$-equivariant networks. Moreover, our method is competitive in an inverse problem benchmark, while employing off-the-shelf ResNet architectures.

On the Convergence Rate of Gaussianization with Random Rotations

Gaussianization is a simple generative model that can be trained without backpropagation. It has shown compelling performance on low dimensional data. As the dimension increases, however, it has been observed that the convergence speed slows down. We show analytically that the number of required layers scales linearly with the dimension for Gaussian input. We argue that this is because the model is unable to capture dependencies between dimensions. Empirically, we find the same linear increase in cost for arbitrary input $p(x)$, but observe favorable scaling for some distributions. We explore potential speed-ups and formulate challenges for further research.

Maximum Likelihood Training of Autoencoders

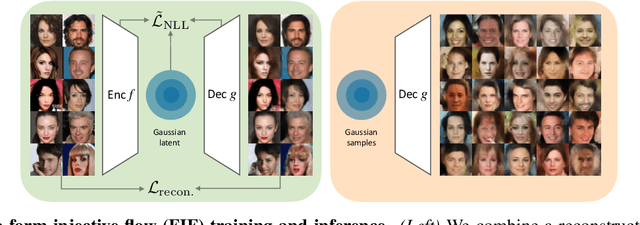
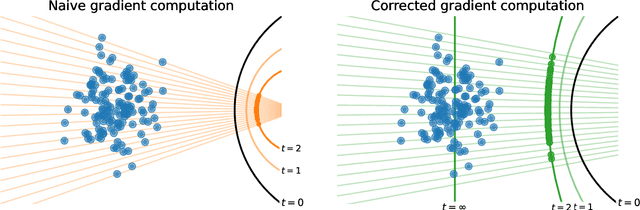
Maximum likelihood training has favorable statistical properties and is popular for generative modeling, especially with normalizing flows. On the other hand, generative autoencoders promise to be more efficient than normalizing flows due to the manifold hypothesis. In this work, we introduce successful maximum likelihood training of unconstrained autoencoders for the first time, bringing the two paradigms together. To do so, we identify and overcome two challenges: Firstly, existing maximum likelihood estimators for free-form networks are unacceptably slow, relying on iteration schemes whose cost scales linearly with latent dimension. We introduce an improved estimator which eliminates iteration, resulting in constant cost (roughly double the runtime per batch of a vanilla autoencoder). Secondly, we demonstrate that naively applying maximum likelihood to autoencoders can lead to divergent solutions and use this insight to motivate a stable maximum likelihood training objective. We perform extensive experiments on toy, tabular and image data, demonstrating the competitive performance of the resulting model. We call our model the maximum likelihood autoencoder (MLAE).

Finding Competence Regions in Domain Generalization

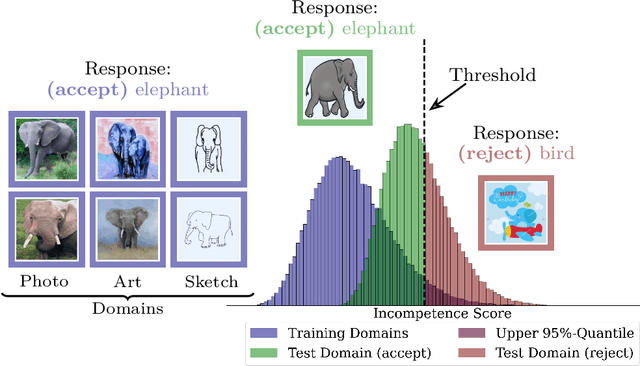
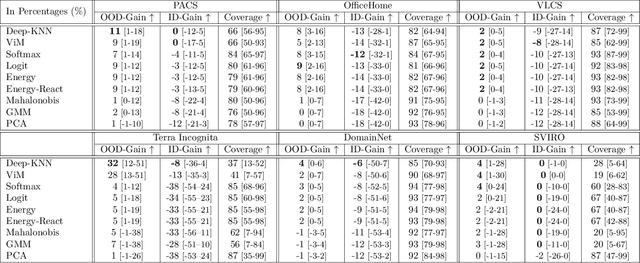
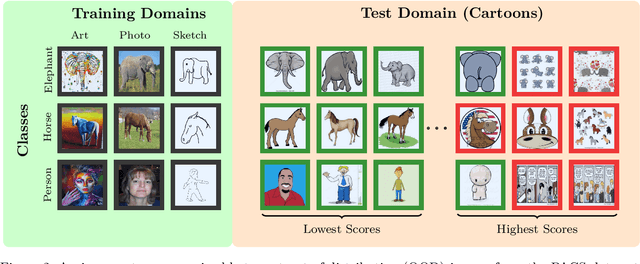
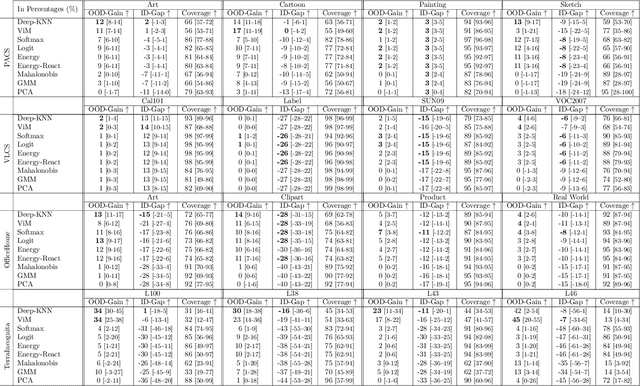
We propose a "learning to reject" framework to address the problem of silent failures in Domain Generalization (DG), where the test distribution differs from the training distribution. Assuming a mild distribution shift, we wish to accept out-of-distribution (OOD) data whenever a model's estimated competence foresees trustworthy responses, instead of rejecting OOD data outright. Trustworthiness is then predicted via a proxy incompetence score that is tightly linked to the performance of a classifier. We present a comprehensive experimental evaluation of incompetence scores for classification and highlight the resulting trade-offs between rejection rate and accuracy gain. For comparability with prior work, we focus on standard DG benchmarks and consider the effect of measuring incompetence via different learned representations in a closed versus an open world setting. Our results suggest that increasing incompetence scores are indeed predictive of reduced accuracy, leading to significant improvements of the average accuracy below a suitable incompetence threshold. However, the scores are not yet good enough to allow for a favorable accuracy/rejection trade-off in all tested domains. Surprisingly, our results also indicate that classifiers optimized for DG robustness do not outperform a naive Empirical Risk Minimization (ERM) baseline in the competence region, that is, where test samples elicit low incompetence scores.

Whitening Convergence Rate of Coupling-based Normalizing Flows

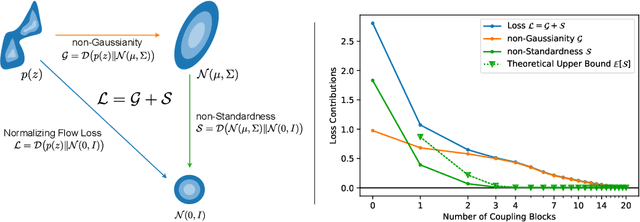
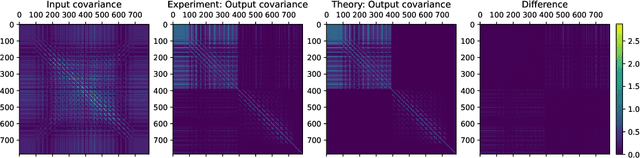
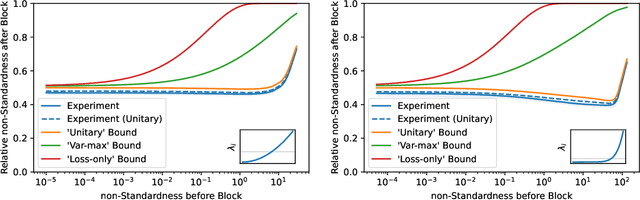
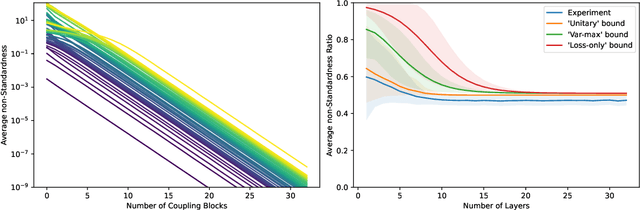
Coupling-based normalizing flows (e.g. RealNVP) are a popular family of normalizing flow architectures that work surprisingly well in practice. This calls for theoretical understanding. Existing work shows that such flows weakly converge to arbitrary data distributions. However, they make no statement about the stricter convergence criterion used in practice, the maximum likelihood loss. For the first time, we make a quantitative statement about this kind of convergence: We prove that all coupling-based normalizing flows perform whitening of the data distribution (i.e. diagonalize the covariance matrix) and derive corresponding convergence bounds that show a linear convergence rate in the depth of the flow. Numerical experiments demonstrate the implications of our theory and point at open questions.